Nearest Neighbor Classification

给定一个查询样本 $q$，找到 k 个离 $q$ 最近的样本点。对于回归任务，返回这 k 个点的均值；对于分类任务，返回数量最多的类别或者分布表

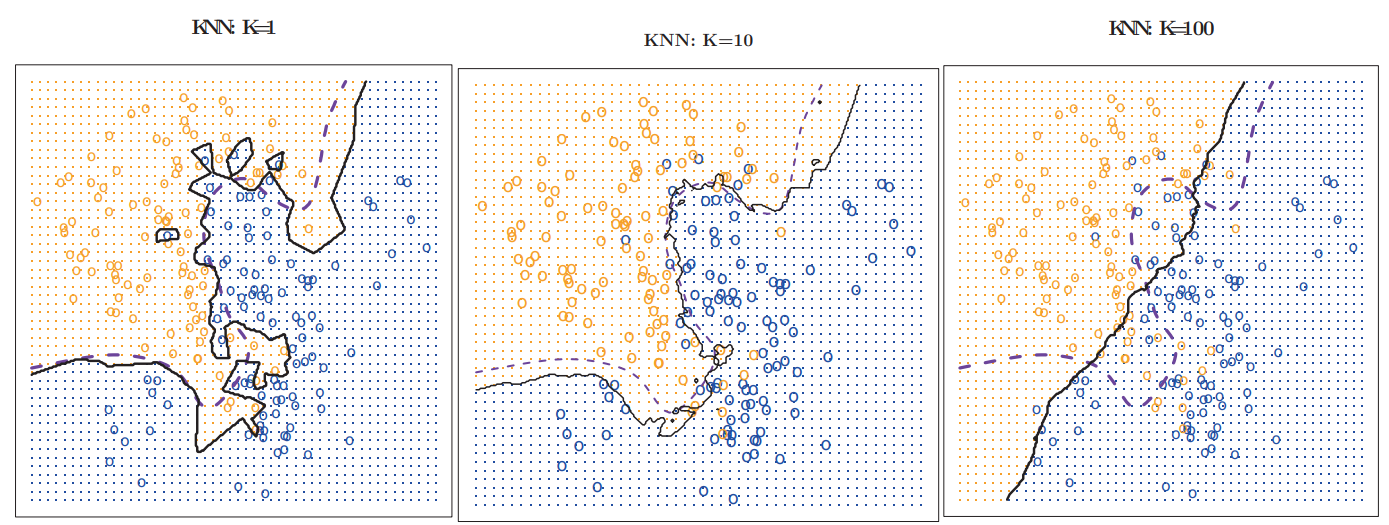
随着超参数 k 的数值增大，kNN 一般会由过拟合变为欠拟合

Exhaustive k-NN 算法

给定一个样本点 $q$，计算所有的 n 个训练样本点到 $q$ 的距离，维护一个距离的小顶堆得到最小的 k 个距离

k-NN 的训练复杂度为 0, 运行复杂度为 $O(nd + n\log k)$

Voronoi Diagrams

设 $X$ 是一个点集，对于 $w \in X$，它的 Voronoi cell 定义为

$X$ 中 所有的 Voronoi cell 就是 Voronoi diagram

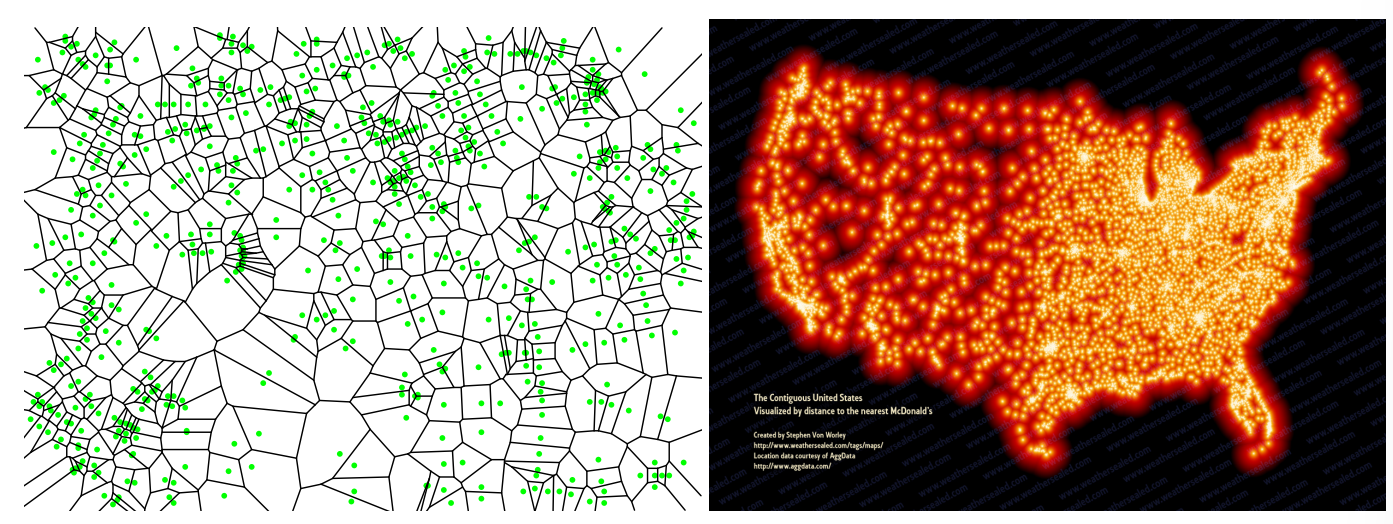
Voronoi diagram 的空间复杂度为 $O(n^{[d / 2]}$（用边来衡量），当维度 d 增加是空间复杂度会稍微低于这个公式，但是仍然是指数级增长，所以不适合于高维数据。但是在实际应用中复杂度一般都是 $O(n)$

在运行时，给定一个点 $q$，找出一个点 $w$ 使得 $q \in Var(w)$，那么我们就可以使用 $w$ 的属性来预测 $q$

对于二维数据，在训练时需要 $O(n\log n)$ 的复杂度计算 Voronoi diagram，并使用一个梯形图（trapezoidal map）存储数据；运行时查找 Voronoi cell 的复杂度为 $O(\log n)$。对于高维数据需要使用 binary space partition tree 来存储，并且复杂度难以衡量

Voronoi 只是用了一个邻近点来估计 $q$，所以是一种 1-NN 算法，虽然可以推广到 k 阶，但是计算复杂度较大且难以实现

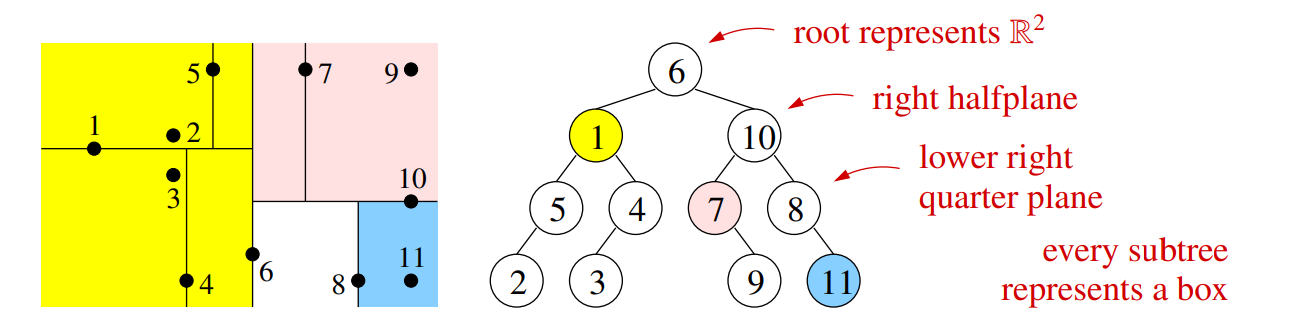
k-d Trees

k-d Tree 使用类似决策树的方式来进行 NN 搜索，但是使用和决策树不同的准则来选择最优划分

• 选择宽度最大的特征 $w$ 用于划分，即特征 i that $\max_{i, j,k}(X_{ji} - X_{ki})$，因为我们不希望一个样本点发散出去的邻接区跨越多个 box 区域，所以在宽度较大的特征上进行切分可以让 box 接近正方形
• 选择特征的中位数或者中值作为划分边界。使用中位数可以保证树的深度为 $\log_2 n$，建树复杂度为 $O(nd \log n)$；如果使用中值可能导致树失衡
• 每个中间节点都会存储一个训练数据点，所以每次搜索的时候不用下降到叶节点

在运行时，给定一个点 $q$，寻找一个训练样本点 $w$ 满足 $\|q - w \| \le (1 + \epsilon) \|q - u\|$，其中 $u$ 是训练样本中距离 $q$ 最近的距离，也就是我们找到的样本点 $w$ 不能远于最小距离的 $1+\epsilon$ 倍

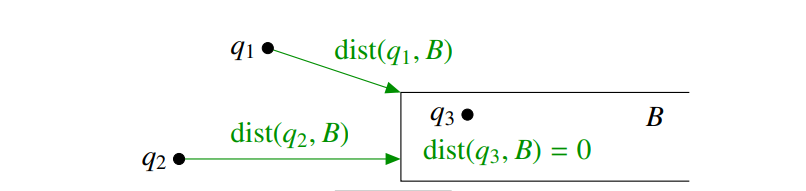
在搜索时，我们需要计算 $q$ 到区域 B 的最小距离 $dist(q, B) = \min_{z \in B} \|q - z\|$

搜索过程中需要维护一个小顶堆，用来保存在还没有搜索的 box 的距离。每次搜索的时候优先搜索离 $q$ 最近的 box。如果当前搜索的 box 离 $q$ 的距离的 $1 + \epsilon$ 倍小于下一个最近 box 则继续，反之停止搜索

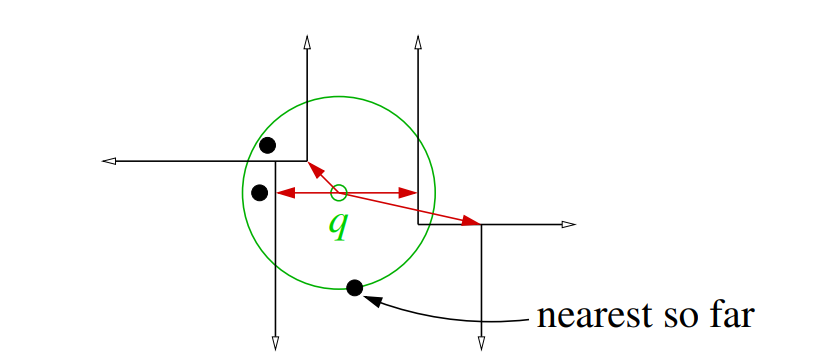
1-NN 算法：

• 将根节点的距离设置为 0，推入小顶堆 $Q$
• 将当前距离 $r$ 设置为 $\infty$
• 如果 $Q$ 不为空，并且 $(1 + \epsilon) \cdot \text{minkey}(Q) > r$
  • 将 $Q$ 中节点弹出，它对应的 box 是 $B$
  • 取出 $B$ 中的训练样本 v，如果 $\|q - v\| < r$，那么 $w \leftarrow v; r \leftarrow \|q - v\|$
  • 继续查看子节点对应的区域 $B'$ 和 $B''$
    • 如果 $(1 + \epsilon) \cdot dist(q, B') < r$，将 $B'$ 和距离插入 $Q$
    • 如果 $(1 + \epsilon) \cdot dist(q, B'') < r$，将 $B''$ 和距离插入 $Q$
• 返回 $w$