AdaBoost
AdaBoost 是一个集成学习方法,它可以降低偏差(Bagging 法可以降低方差)
AdaBoost 使用不同权重的训练样本训练学习器,如果某个样本被错误分类,那么它的权重将增加;并且对每个学习器使用不同的权重,更加准确的学习器施加更大的权重
假设我们训练 T 个分类器 $G_1, \dots, G_T$,训练样本 $X_i$ 在训练 $G_t$ 是的权重取决于 $G_1, \dots, G_{t-1}$ 错误分类它的次数,此外如果 $X_t$ 被一个非常精准的分类器分类错误,它的权重将会增加的更多,每次 $X_i$ 被正确分类,它的权重也会相应缩小。
组合学习器(Metalearner)是所有学习器的线性组合,即 $M(z) = \sum_{t = 1}^T \beta_t G_t(z)$,虽然每个学习器 $G_t$ 的输出是二元的分类,但是组合学习器的输出是连续的值
在第 T 步时,我们需要选择一个新的学习器 $G_T$ 和对应的权重 $\beta_T$,为了实现最优选择,首先选定风险为
$$Risk = \frac{1}{n} \sum_{i = 1}^n L(M(X_i), y_i)$$其中 AdaBoost 的损失函数为
$$ L(\hat{\lambda}, \lambda) = e^{- \hat{\lambda}\lambda} = \begin{cases} e^{-\hat{\lambda}} \quad \lambda = + 1 \\ e^{\hat{\lambda}} \quad \lambda = -1 \end{cases} $$我们对风险推导可得
$$ \begin{align*} n \cdot Risk &= \sum_{i = 1}^n L(M(X_i), y_i) = \sum_{i = 1}^n e^{-y_i M(X_i)} \\ &= \sum_{i = 1}^n \exp \left( -y_i\sum_{i = 1}^T \beta_t G_t(X_i) \right) = \sum_{i = 1}^n \prod_{t = 1}^T e^{-\beta_t y_i G_t(X_i)} \\ &= \sum_{i = 1}^n w_i^{(T)} e^{-\beta_T y_i G_T(X_i)} , \quad where \quad w_i^{(T)} = \prod_{t = 1}^{T - 1} e^{-\beta_t y_i G_t(X_i)} \\ &= e^{-\beta_T} \sum_{y_i = G_T(X_i)} w_i^{(T)} + e^{\beta T} \sum_{y_i \ne G_T(X_i)} w_i^{(T)} \\ &= e^{-\beta_T} \sum_{i = 1}^n w_i^{(T)} + (e^{\beta_T} - e^{-\beta_T}) \sum_{y_i \ne G_T(X_i)} w_i^{(T)} \end{align*} $$其中 $w_i^{(T)} = \prod_{t = 1}^{T - 1} e^{-\beta_t y_i G_t(X_i)}$ 只与 $G_1, \dots, G_{T -1}$ 有关,可以看作风险中每个样本的权重,并且该样本在前面几轮中被分错的次数越多,$w_i^{(T)}$ 越大
同时,我们也可以得到 $w_i^{(T)}$ 的递推公式
$$ w_i^{(T + 1)} = w_i^{(T)} e^{-\beta_T y_i G_T(X_i)} = \begin{cases} w_i^{(T)} e^{-\beta T} \quad y_i = G_T(X_i) \\ w_i^{(T)} e^{\beta_T} \quad y_i \ne G_T(X_i) \end{cases} $$在风险的最终形态中,第一项 $e^{-\beta T} \sum_{i = 1}^n w_i^{(T)}$ 只与上面的几个分类器有关,所以在第 T 轮想要风险最小,就要最小化第二项中的 $\sum_{y_i \ne G_T(X_i)} w_i^{(T)}$,也就是所有被分类错误的样本的权重 $w_i^{(T)}$。所以在每一轮中选择 $G_T$ 的准则就是让分类错误的样本的权重之和最小。虽然决策树一般可以将所有的样本点都分类正确,但是 boosting 中一般只会使用较短、非理想的决策树
在选择 $\beta_T$ 时,令 $\frac{d}{d \beta_T}Risk = 0$, 即
$$0 = -e^{\beta_T} \sum_{i = 1}^n w_ii^{(T)} + (e^{\beta_T} + e^{-\beta_T}) \sum_{y_i \ne G_T(X_i)} w_i^{(T)}$$令
$$err_T = \frac{\sum_{y_i \ne G_T(X_i)}w_i^{(T)}}{\sum_{i=1}^n w_i^{(T)}}$$将 $err_T$ 称为 weighted error rate,可以算出
$$\beta_T = \frac{1}{2} \ln \left( \frac{1 - err_T}{err_T} \right)$$从上式可以看出,如果 $err_T = 0$ 那么 $\beta_T = \infty$,如果 $err_T = 1 / 2$ 那么 $\beta_T = 0$,也就是说如果一个学习器的 error 为 50%, 则它将对组合学习器无贡献
更具上面的讨论我们就可以得到 AdaBoost 算法:
- 初始每个训练样本的权重 $w_i \leftarrow \frac{1}{n},\forall{i} \in [1, n]$
- for 循环 1 至 T
- 计算加权错误率 $err = \frac{\sum_{mis} w_i}{\sum_{all} w_i}$,以及系数 $\beta_t = \frac{1}{2} \ln \left( \frac{1 - err}{err} \right)$
- 更新权重 $w_i \leftarrow w_i \cdot \begin{cases} e^{\beta_T}, \quad G_t(X_i) \ne y_i \\ e^{-\beta_t}, \quad other \end{cases} = w_i \cdot \begin{cases} \sqrt{\frac{1 - err}{err}} \\ \sqrt{\frac{err}{1 - err}} \end{cases}$
- 返回组合学习器 $h(z) = sign\left( \sum_{t = 1}^T \beta_t G_t(z) \right)$
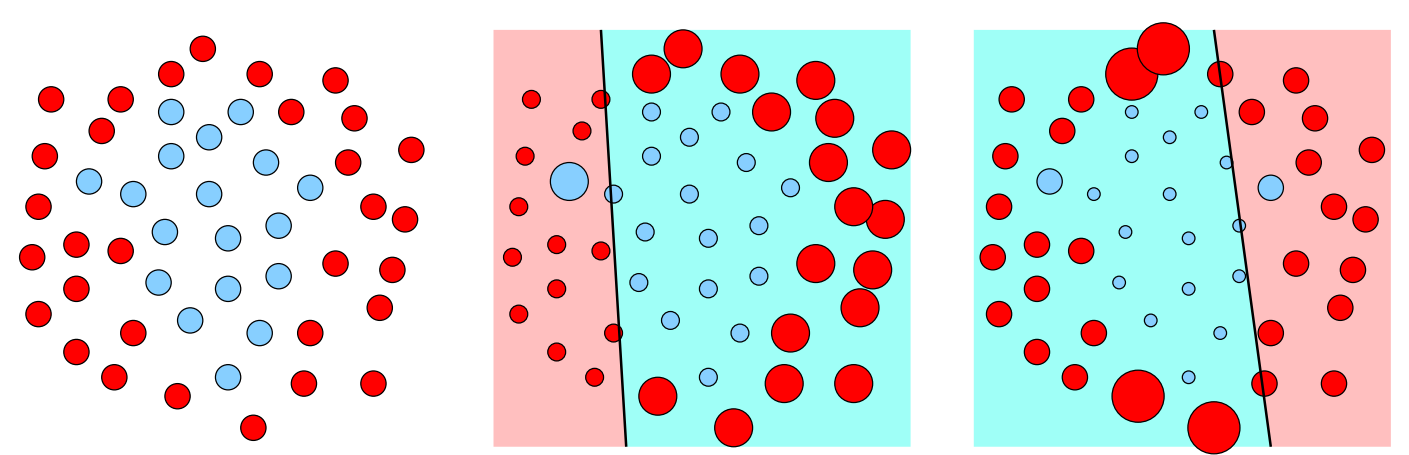
如上图所示,初始时我们为每个训练样本施加相同的权重,然后根据分类器分类正确与错误的情况减小或者增加权重
为何 boost 往往搭配决策树,并且使用较短的树结构
- Boosting 可以减小偏差,但是不一定会减小方差,使用较短的树结构主要是为了防止过拟合
- 树的训练一般较快,而在 boosting 法下我们需要训练多个学习器
- 决策树不需要超参数
- AdaBoost 加上短树相当于是一种特征子集选择,无法提高 metalearning 估计能力的特征完全没有使用(err 为 50% 的)
- 线性决策边界和 boost 的组合并不好
