梯度消失与爆炸
当使用 sigmoid 函数时,如果 sigmoid 的输出接近 0 或 1,那么梯度 $s' = s(1 - s) \approx 0$,此时梯度更新将会特别缓慢,这个问题被称为梯度消失,在深层网络中,反向传播会使得梯度消失加剧
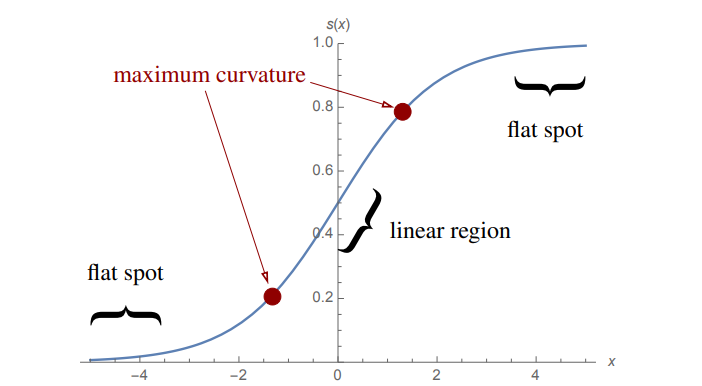
将激活函数换为 ReLU 将会缓解梯度消失,ReLU 的定义为 $r(\gamma) = max\{0, \gamma\}$,它的导数为
$$ r'(\gamma) = \begin{cases} 1, \quad \gamma \ge 0, \\ 0, \quad \gamma < 0 \end{cases} $$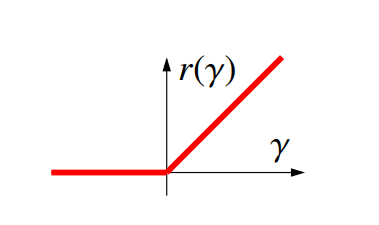
在现代神经网络中,ReLU 一般被用于中间层的激活函数,因为 ReLU 的梯度很少全部为 0,更多的情况是部分神经元的梯度为 0
然而 ReLU 的输出可以无限大,带了梯度爆炸问题,特别是在深层网络中,大输入造成了梯度随着网络深度不断变大
输出层
ReLU 一般被使用于隐藏层,而在输出层一般为线性单元(回归问题)或者 sigmoid/softmax 单元(分类问题),分别对应了线性回归、logistic 回归和 softmax 回归
