神经网络
单个的、基础的感知机存在严重局限性,无法解决像 XOR(异或)这样看似简单但非线性的问题。如下图,异或的二维输入和输出表示了三维空间的点,无法被线性分类器分类
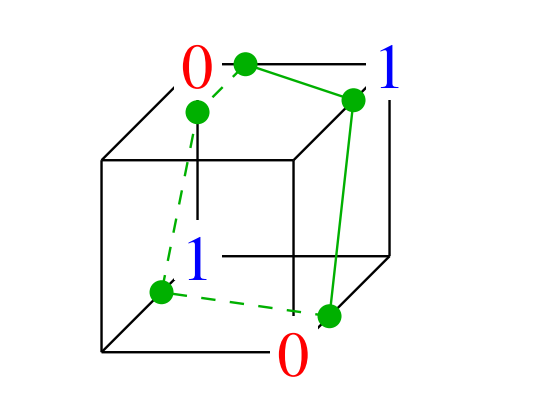
如果添加一个二次特征 $x_1x_2$,那么 XOR 将在 3 维空间线性可分
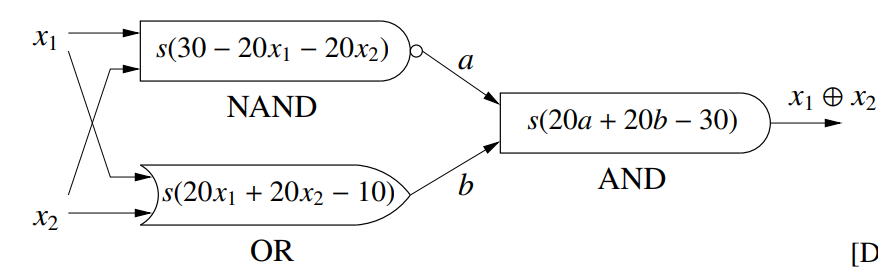
当然,我们也有更佳的方法,通过多个单层线性分类器的叠加可以实现类似电路的逻辑连接,此外在每个线性分类器的输出添加一个非线性的函数 $s$ 可以实现类似电路逻辑门。所以通过多个线性连接+非线性函数(一般为 logistic 函数)可以轻易实现异或,其中每个线性线性连接+非线性函数组成了一个神经元
一层隐藏层的网络
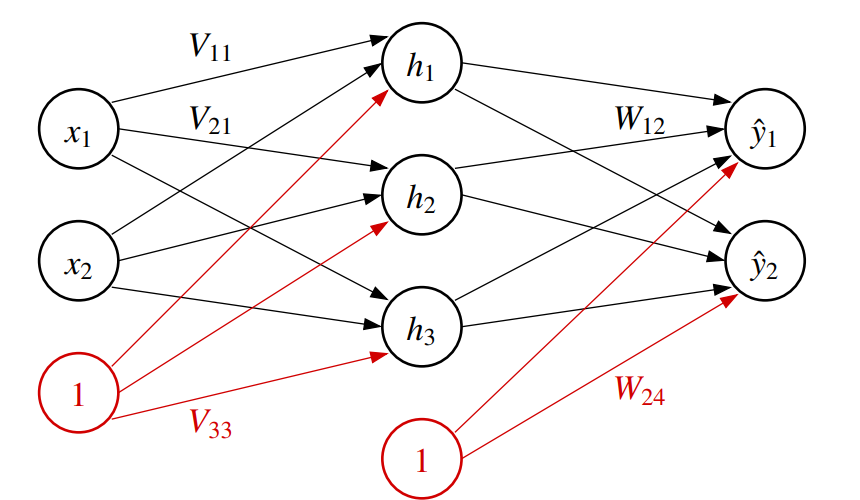
多个神经元组成的三层网络如同
集合函数 $s(\gamma) = \frac{1}{1 + e^{-\gamma}}$,被称为激活函数。对于一个向量 $u$,定义 $s(u) =\begin{bmatrix}s(u_1) \\ s(u_2) \\ \vdots\end{bmatrix}$,$s_1(u) = \begin{bmatrix} s(u_1) \\ s(u_2) \\ \vdots \\ 1\end{bmatrix}$ 表示包含偏置的形式
那么有
$$ \begin{align*} h &= s_1(Vx) \\ \hat{y} &= s(Wh) = s(Ws_1(Vx)) \end{align*} $$神经网络可以有多个输出节点,所以我们可以基于相同的隐状态训练多个分类器,有时候不同的分类器可以使用不同隐藏层神经元,并且多个分类器的结果可以互相补充
训练
神经网络的训练一般使用随机梯度下降或者批梯度下降
选择损失函数 $L(\hat{y}, y)$,例如 $L(\hat{y},y) = \|\hat{y} - y\|^2$, 寻找 $V$ 和 $W$ 可以最小化成本函数 $J(V,W) = \frac{1}{n} \sum_{i = 1}^n L(\hat{y}(X_i), Y_i)$
神经网络的成本函数一般不是凸函数,存在非常多的局部最小值(local minima),一般可以通过增加更多的隐藏节点缓解这个问题
神经网络的节点具有对称性,不同神经元之间结构一致,如果所有的神经元都初始化为相同点权重,那么所有的输出和梯度都一致,所有的神经元在参数更新中都会保持一致,所以一般使用随机权重初始化神经元
神经元的权重不能初始化为过大或者过小,否则会处于 logistic 函数的饱和区,梯度过小
梯度计算
我们可以使用链式法则求每个节点的梯度
对于公式 $f=((a + b) c)^2$,可以将其拆解成链式传播的形式,然后从 $f$ 开始逐次求解每个节点的梯度
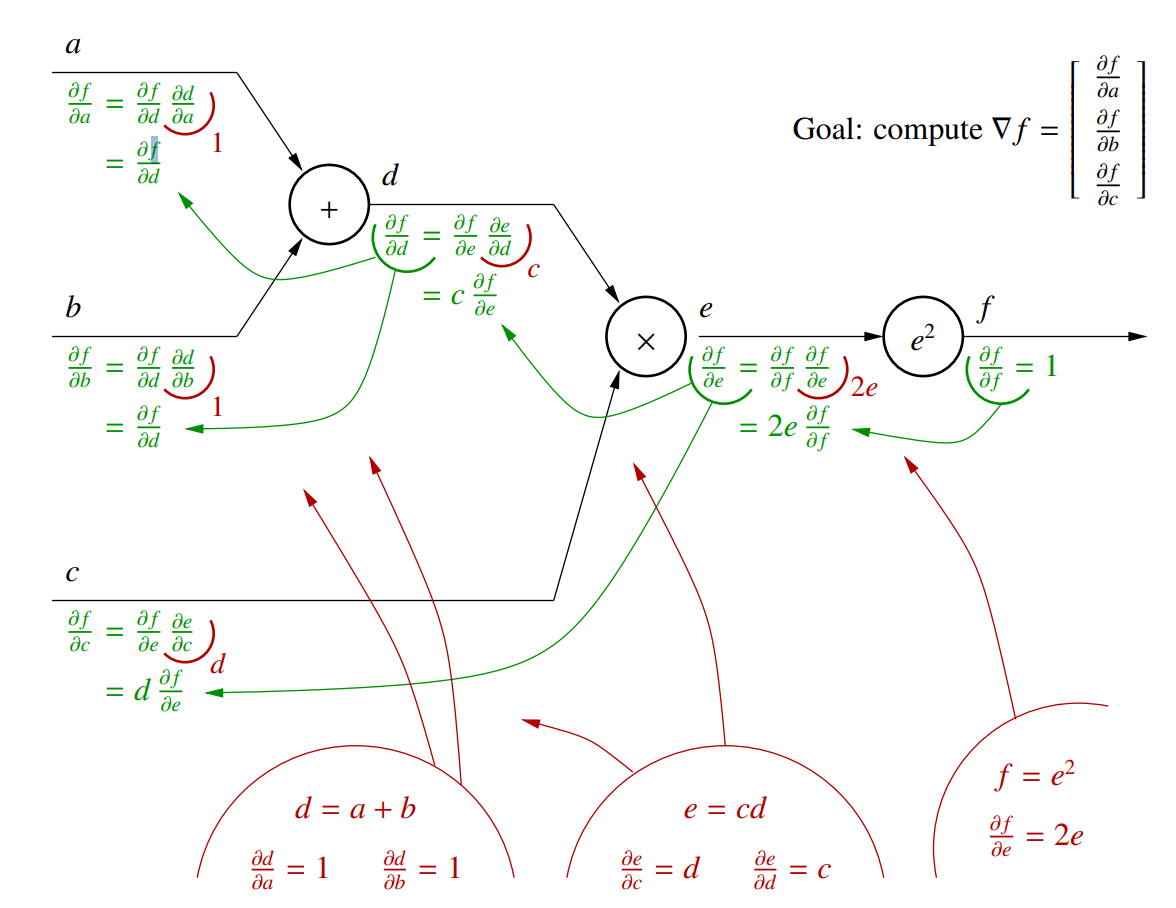
对于多元数据,同样可以使用多元微分
$$\frac{\partial}{\partial \alpha} L(y_1(\alpha), y_2(\alpha)) = \frac{\partial L}{\partial y_1} \frac{\partial y_1}{\partial \alpha} + \frac{\partial L}{\partial y_2} \frac{\partial y_2}{\partial \alpha} = \nabla_y L\cdot \frac{\partial}{\partial \alpha} y$$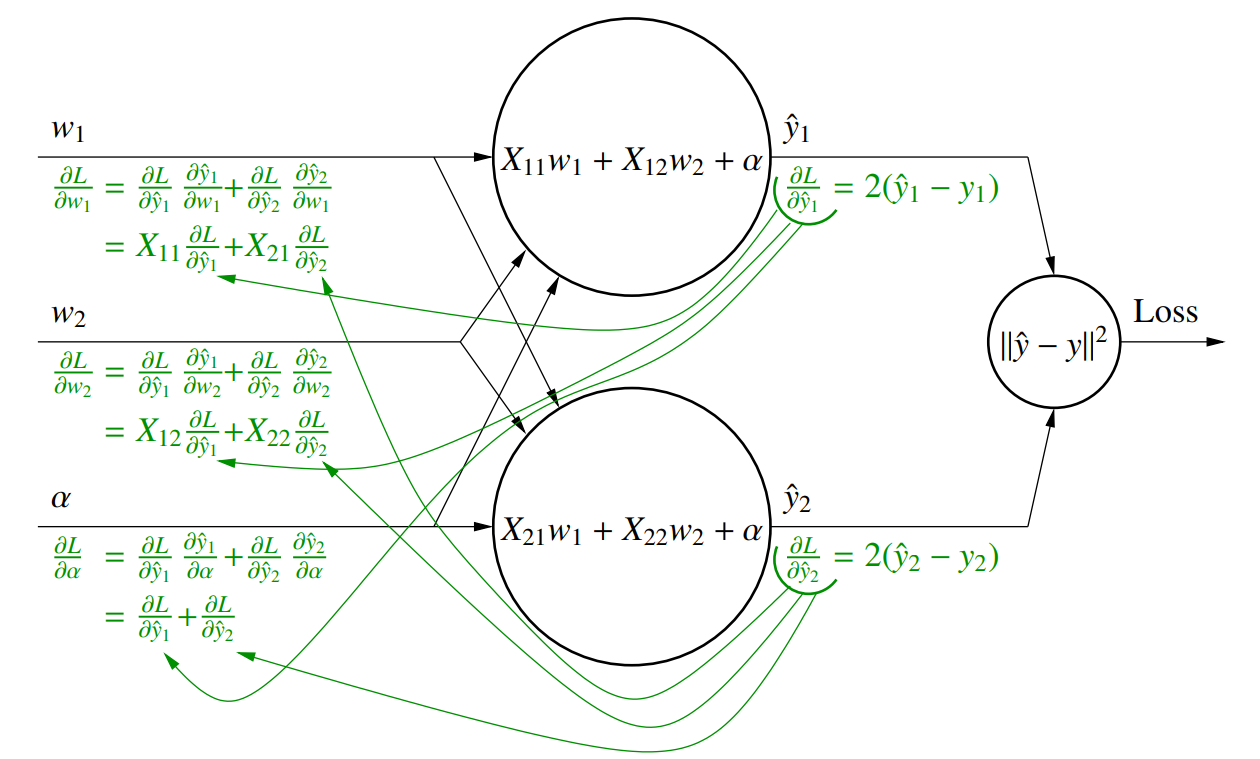
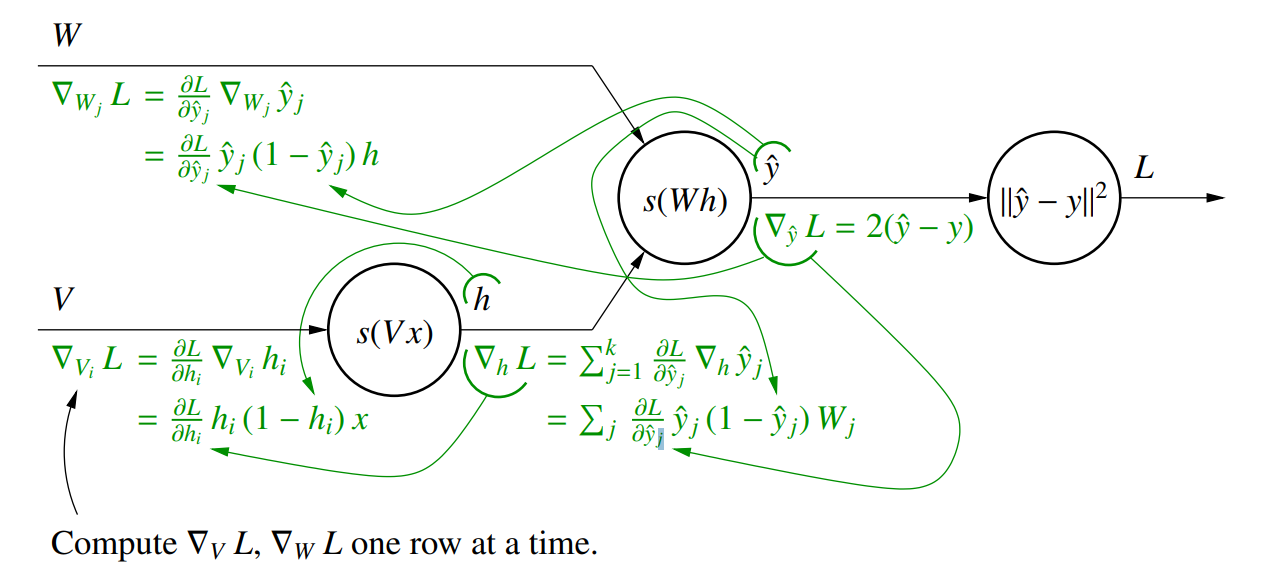
同样我们也可以通过链式法则求成本函数,梯度计算是从后往前进行的,被称为反向传播算法