决策树的变种
决策树回归
决策树回归就是通过一系列是否问题,创建了一个分段常数函数(Piecewise Constant Regression Fn),在函数的每一段,决策树的预测是一个固定的常数
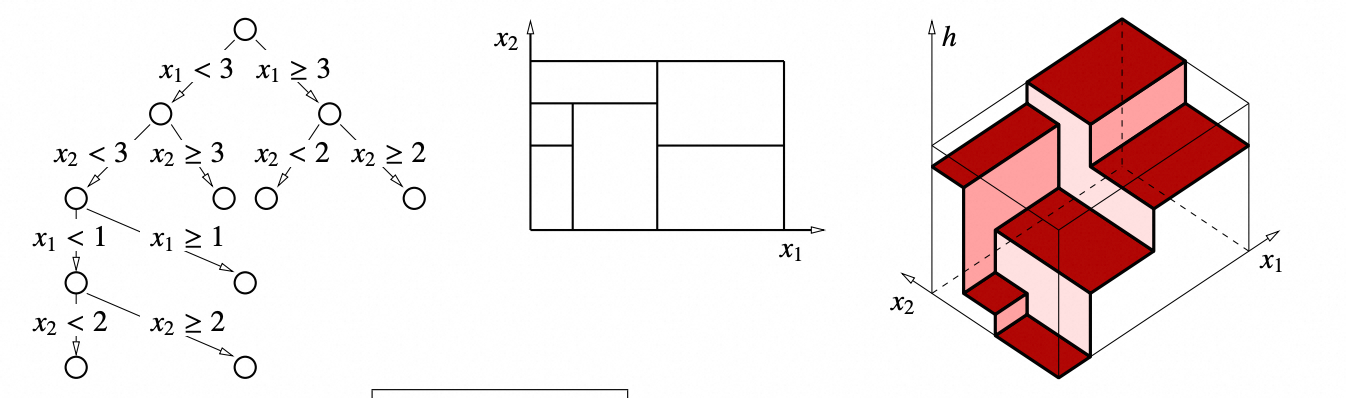
- 上图左边是一个对特征维度为 2 的样本进行决策回归的过程,数据顺着路径到达某一个叶子节点得到最终的预测值
- 中间的图表示决策树将整个特征空间划分成多个区块,每个区块对应一个叶子节点
- 右图表示对应的分段常数函数,每个特征空间中的区块都对应了一个常数的叶子节点预测值
每一个叶子节点的预测值,由落入这个叶子节点的所有样本的值的平均决定,即
$$\mu_S = \frac{1}{|S|}\sum_{i \in S}y_i$$其中 $S$ 表示落入某个节点的样本索引的集合
决策树的目标是使分裂后的子区域纯度尽可能高。对于分类数,目标是让子区域的类别尽可能一致;对于回归树,我们希望让子区域的样本真实值 $y$ 尽可能接近
所以我们可以使用子区域内样本的方差作为 cost
$$J(S) = Var(\{ y_i: i\in S \}) = \frac{1}{|S|} \sum_{i \in S} (y_i - \mu_S)^2$$所以每次选择可以使得划分出的两个子集方差的加权平均(根据样本点树加权)最小的划分点
早停
在构造决策树的时候,没必要让每个叶节点到达纯净,可以实现加速以及防止过拟合
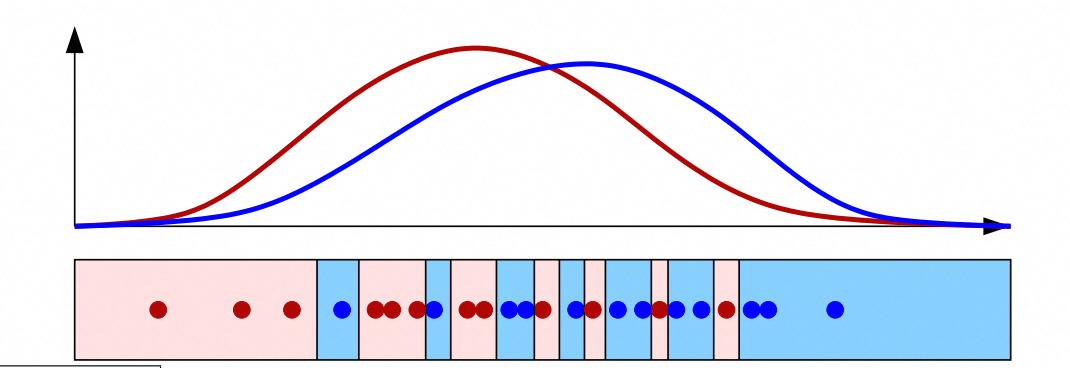
对于上图两个重合非常大的概率分布,得到一个叶子节点的纯净决策树一定会造成过拟合
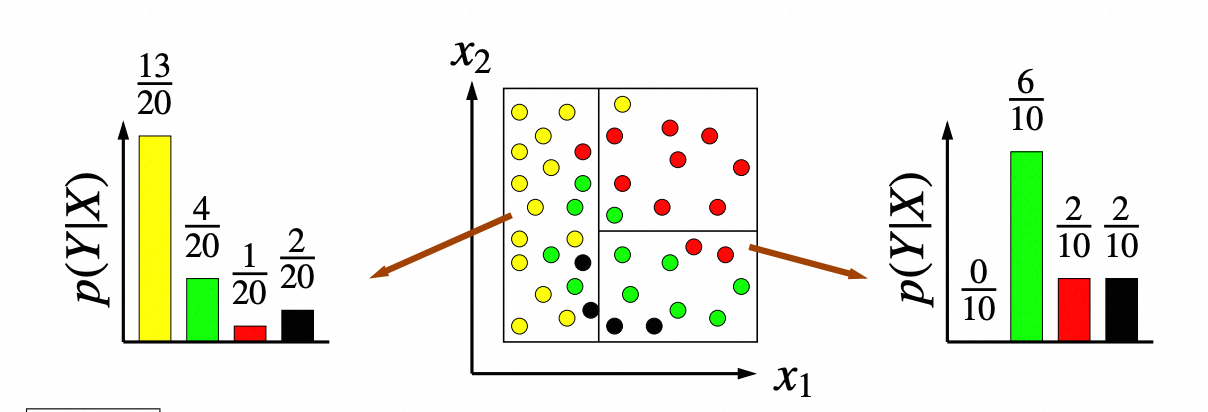
此外叶子节点不那么纯净,往往能包含更加丰富的信息。例如,对于上图的决策树划分,我们可以通过统计每个子区域内不同类别的点数,得到某种类别被分到该叶子节点的概率。对于分类树,直接去概率最大的类别最为叶子节点输出的类别;对于回归树,使用平均值作为叶子节点的预测值
决策树可以使用的早停策略包括:
- 继续划分不再降低熵或者误差(有可能一直划分到纯净节点)
- 大多数(例如大于 90%)节点类别相同
- 节点包含的样本点过少(例如小于 10)
- 子区域过小
- 树的深度太大
- 使用验证集检验
剪枝
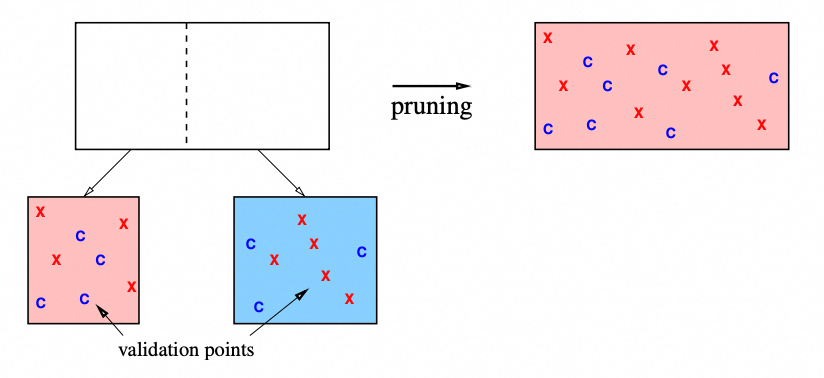
如果树太大,可以通过移除一些划分来提高在验证集的表现
剪枝往往比早停更加有效,因为有时候某次划分带来的提升不明显,但是接下来可能出现提升明显的划分
在剪枝时,如果每次去除一个分割后重新从头计算验证集指标会造成非常大的开销。相反,我们应该在构建深度树的时候记录下每个节点中包含了哪些样本,这样剪枝的时候只需将子节点的样本合并到父节点
多变量划分
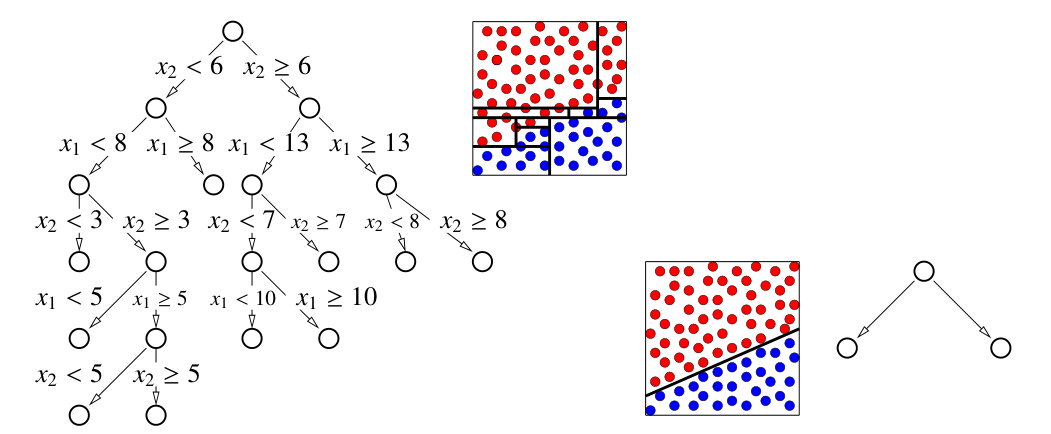
一个标准的决策树一次只对一个特征进行划分(如左图),对于 SVM 可以轻易区分的斜线,决策树需要学习一个非常复杂的规则
如果想要使用多个特征进行划分,可以在每个节点使用例如 SVM、逻辑回归和高斯判别分析,这些分类器通过决策树的层级结构可以学习到非线性的决策边界
集成学习 Ensemble Learning
决策树快、简单并且可以解释性强,但是方差较大。例如,如果将两个数据集分成两份,分别训练两个决策树,这两个决策树可能差异非常大,特别是如果根节点选择的划分特征不同的时候
我们可以通过集合多个弱估计器,来得到一个强估计器,如果一个弱估计器的方差较大,那么将多个弱估计器组合去平均将会大大降低方差
为了得到一个强估计器,可以使用不同的方法取平均:
- 不同的学习算法
- 使用不同数据集训练的同一算法
- bagging 法:使用一个数据集的不同随机子采样训练同一算法
- 随机森林:使用一个数据集的不同随机子采样训练随机决策树
平均可以很好的降低方差,但是无法降低偏差,所以我们需要在平均之前得到一些小偏差的估计器(即使存在一定程度的过拟合也没问题)
Bagging
Bagging 是一种使用一个数据集训练多个不同学习器的方法,它对大多数算法都有效(kNN 除外)
给定一个 $n$ 点的训练样本集,从里面又放回地随机选取 $n'$ 个样本,这意味着某些样本被多次采样。如果 $n' = n$,那么大概有 63.2%的样本被采样
Bagging 法存在一个问题:某些样本被采样了 $j$ 次,所以他们在训练数据中占有更大的比重
随机森林
仅仅使用 Bagging 法加上决策树仍然不够,因为可能不同的树模型非常相似。例如,某个特征非常强,那么不同的树都会从它开始划分
为了得到不同的决策树,对于每个节点,随机选取 $m$ 个特征,从这 $m$ 个特征中一个可以最佳划分的特征。其中 $m$ 是超参数,$m$ 越小越随机,不同树之间越不相关,偏差更大
