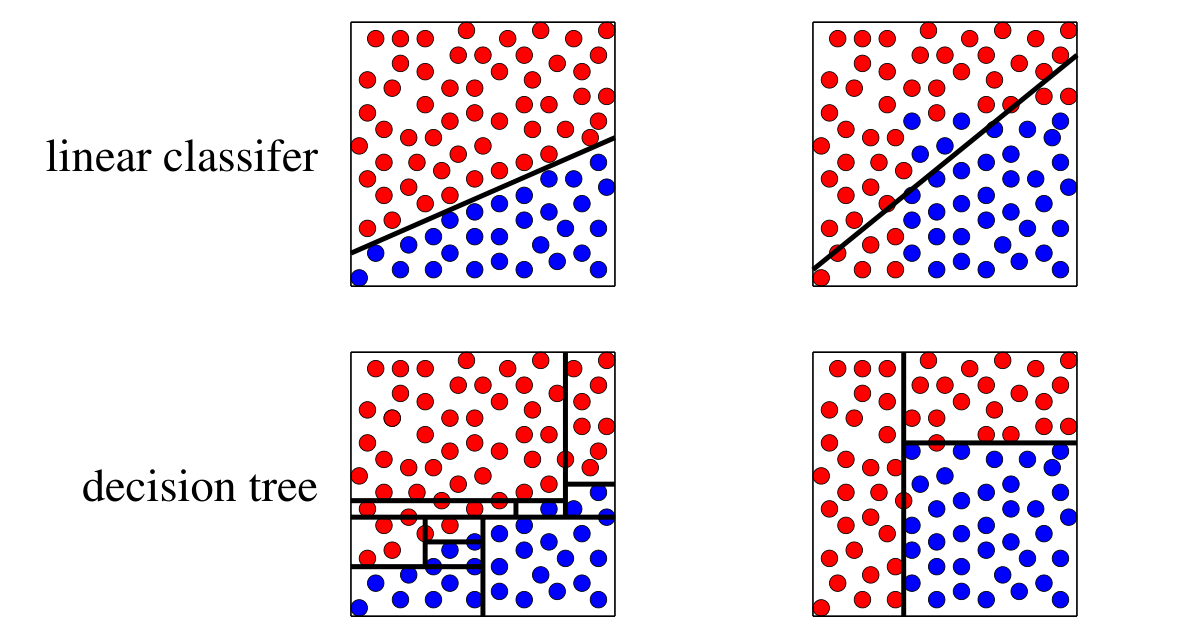
决策树是一种用于分类和回归的非线性方法
决策树有两种节点状态:
- 内部节点:对特征值进行测试(通常是一个),并决定走向哪个分支
- 叶节点:确定最终的类别
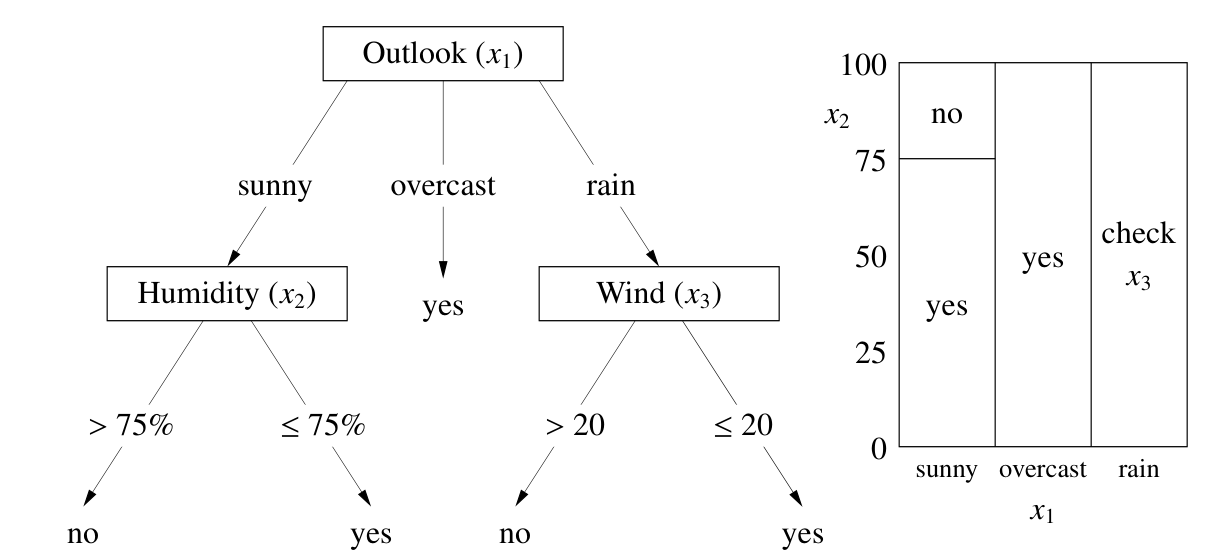
决策树对类别特征和数值特征都较为有效,并且可解释性强,上图是决策树的工作模式。如右图所示,决策树将 x-空间划分成了长方形区块,不过不同程度的分支组合,决策树的决策边界可以任意复杂
设 $X$ 是一个 $n\times d$ 设计矩阵,$y\in \mathbb{R}^n$ 是标签,$S \in \{ 1, 2, \dots, n\}$ 是采样点的索引
决策树的构造
$$ \begin{aligned} &\text{Build Decision Tree} \\ &\text{Procedure } GrowTree(S) \\ &\quad \text{if }(y_i = C \text{ for all } i \in S) \\ &\quad \quad \text{return new } Leaf(C) \\ &\quad \text{else} \\ &\quad \quad \text{choose best splitting feature } j \text{ and splitting value } \beta \\ &\quad \quad S_l = \{i \in S: X_{ij} < \beta\} \\ &\quad \quad S_r = \{i \in S: X_{ij} \ge \beta \} \\ &\quad \quad \text{return new } node(j, \beta, GrowTree(S_l), GrowTree(S_r) \\ &\quad \text{end if} \\ &\text{end procedure} \\ \end{aligned} $$其中的关键是如何选择最优的划分
- 尝试所有可能的划分
- 对于一个集合 $S$,定义它的成本为 $J(S)$ (用来衡量 S 的混乱程度,目标是划分后,子集尽可能纯洁)
- 选择一个划分可以最小化 $J(S_l) + J(S_r)$ (或加权平均 $\frac{|S_l|J(S_l) + |S_r|J(S_r)}{|S_l| + |S_r|}$)
现在我们只需要确定如何计算成本 $J (S)$
方案一:假设 $S$ 中类别最多的类别是 $C$,那么定义 $J (S)$ 为 $S$ 中不属于类别 $C$ 的样本个数
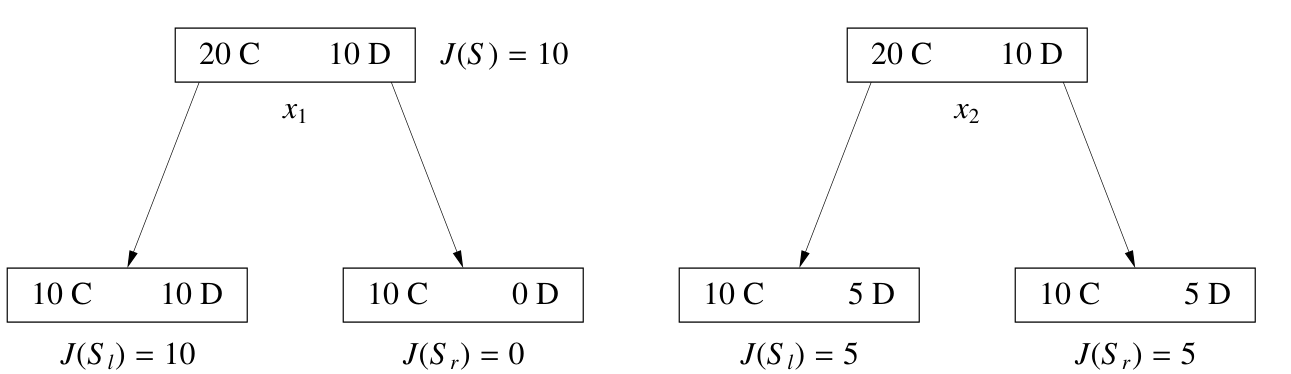
但是对于上图这种划分,最后都能得到 $J(S_l) + J(S_r) = 10$ 的结果,但是左边的更好(划分后类别更纯净), $\frac{|S_l|J(S_l) + |S_r|J(S_r)}{|S_l| + |S_r|}$ 甚至会优先选择右边
方案二:衡量熵
假设 $Y$ 是一个随机类别变量,$P (Y = C) = p_C$,那么 $Y$ 属于 $C$ 的惊讶度(degree of suprise)是 $-\log_2p_C$(如果一个非常可能发生的事发生了,我们并不惊讶;如果不太可能发生的事发生了,我们非常惊讶,它的信息量更大)
那么集合 $S$ 的熵为
$$H(S) = - \sum p_C \log_2 p_C, \quad p_C = \frac{|\{ i \in S: y_i = C\}|}{|S|}$$熵代表了在均匀分布下随机采样的子集 $S$ 中,为了正确识别它的类别,我们需要传输的信息量
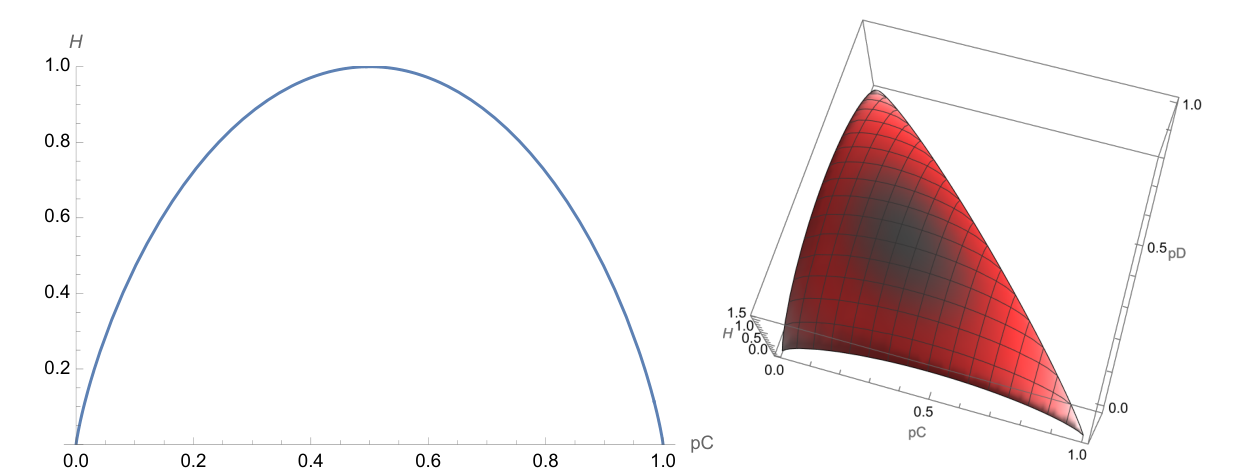
上图分别是两个类别和三个类别的条件下,熵随着类别概率变化的曲线,可以看出如果一个集合中类别约纯净,它的熵越小
在每次划分时,我们可以计算划分后的平均熵
$$H_{after} = \frac{|S_l|H(S_l) + |S_r|H(S_r)}{|S_l| + |S_r|}$$那么我们选择划分的准则就是最大化信息增益 $H(S) - H_{after}$,也就是最小化 $H_{after}$
信息增益将会永远大于等于 0,当某一个子集为空或者所有子集内部类别分布完全一致时,信息增益为 0
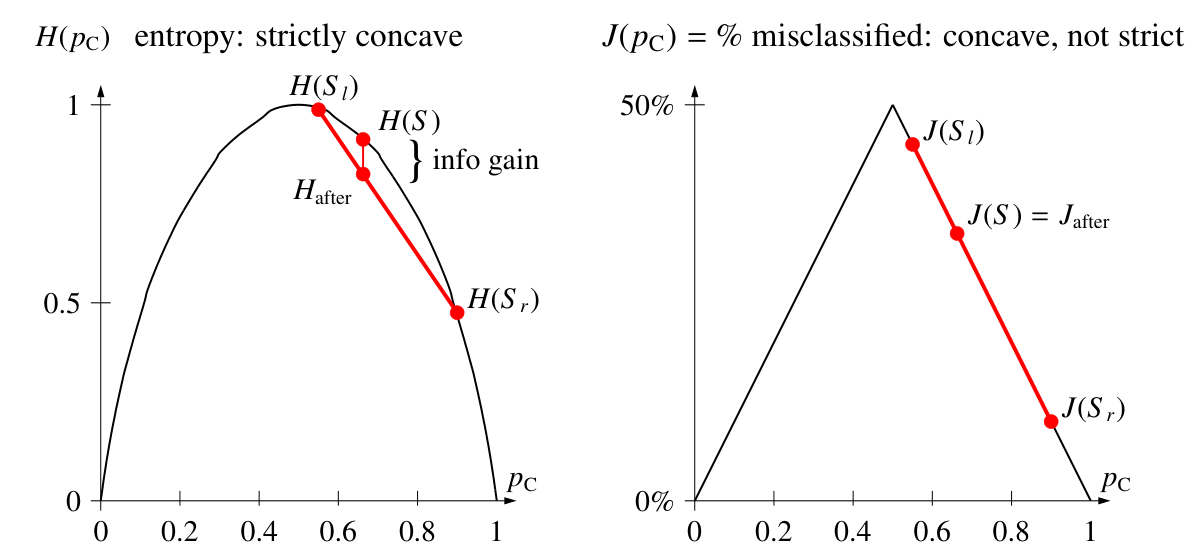
左图是使用熵作为成本函数的划分,可以看到,熵随 $p_C$ 的变化曲线是严格凸的,父节点的熵永远大于两个自节点熵的加权平均;左图是使用 $J(S)$ 作为成本函数的曲线,在很多情况下划分前后的成本相同,无法衡量划分好坏
- 对于二元特征 $x_i$,直接划分成 $x_i = 0$ 和 $x_i = 1$ 两类
- 如果 $x_i$ 有三个或者以上的离散值,可以二元分裂,也可以多元分裂
- 如果 $x_i$ 是一个数值,需要在每两个不同值间尝试分裂点
为了加速计算,我们首先对数值进行排序(如下图),每两个不同值之间都存在一个分裂点(竖线),使用不同的分裂点只会将一个样本从右侧移动到左侧,所以只需初始一次排序,后续记录不同类别的数量变化,这样从左到右改变分裂点时只需要 $O (1)$ 的时间重新计算熵
决策树的计算复杂度:
- 在测试阶段。从根节点到叶节点,最多走完树的深度,复杂度 $\le O(\log n)$
- 在训练阶段。
- 对于每个节点。如果是二元特征,每个节点需要依次尝试利用 $d$ 个特征划分,复杂度为 $O (d)$;如果是数值特征,每个特征如果有 $n'$ 个分裂点,那么复杂度为 $O (n'd)$
- 对于整个树。每个样本点参与 $O (depth)$ 个节点(从上至下),每个样本点在每个节点的计算复杂度为 $O(d)$($n'd$ 平均到 $n'$ 个点),总共有 $n$ 个样本点,所以训练复杂度 $\le O(nd \cdot depth)$
