岭回归 Ridge Regression
岭回归即是最小二乘线性规划加上 $l_2$ 正则化,可以描述为:
寻找一个 $w$,最小化 $J(w) = \|Xw - y\|^2 + \lambda \|w'\|^2$
其中,$w'$ 是使用 0 替代了 $w$ 中对应常数项权重的 $\alpha$ (不用对常数项进行惩罚)
加入 $l_2$ 范数惩罚 $\lambda \|w'\|^2$ 会鼓励参数学习向着 $\|w'\|$ 较小的方向进行,原因如下:
- 保证了代价函数是一个正定二次型,从而有唯一最优解1
- 通过降低方差防止过拟合
如果权重过大,细微的数据动荡将会造成较大的变化
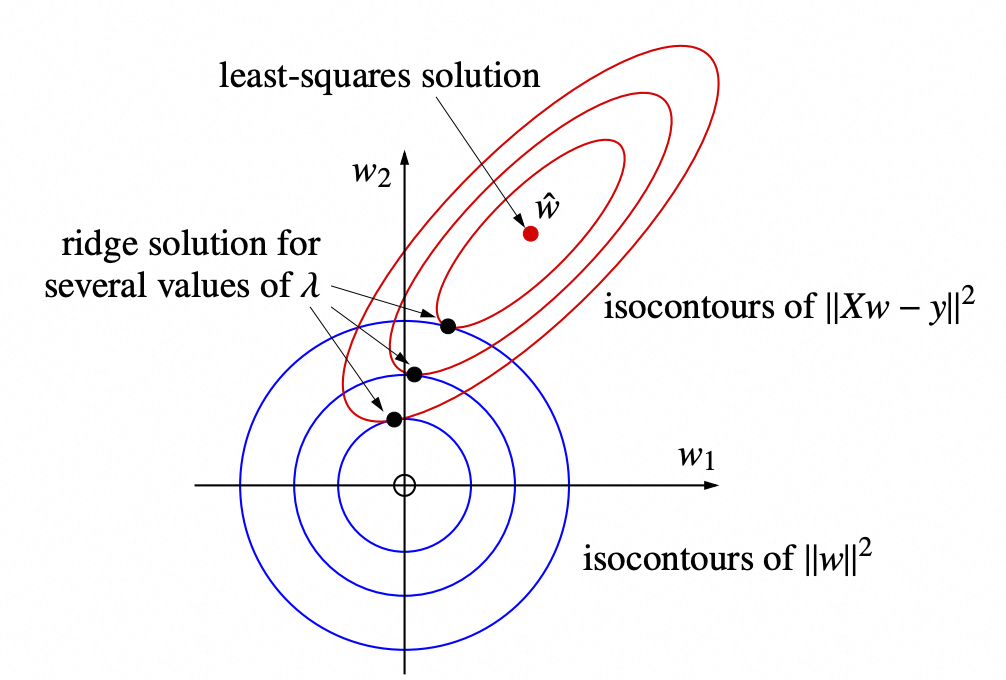
上图中红色的表示 $\|Xw - y\|^2$ 的等值线,蓝色的表示 $\|w\|$ 的等值线,红色等值线第一次和蓝色等值线相交的点就是岭回归的解
可以通过使代价函数的梯度为 0 得到最优 $w$,即求解线性方程组
$$(X^TX + \lambda I')w = X^T y$$其中 $I'$ 是一个特殊的单位矩阵,它的右下角元素被设为 0(不对常数项偏置惩罚)
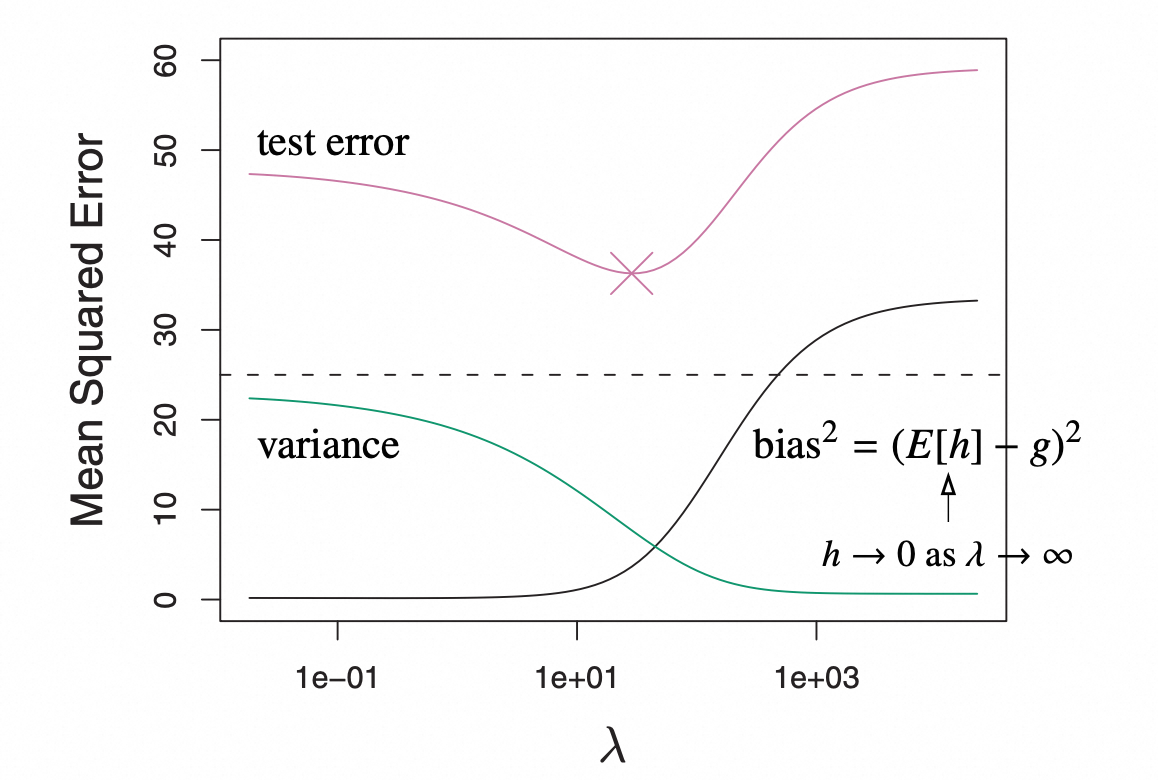
岭回归的方差为 $Var(z^T(X^TX + \lambda I')^{-1} X^T e)$,可以看出 $\lambda$ 增大时,方差减小,但是偏差会增大
岭回归的贝叶斯解释
假设$w'$的先验概率满足 $w' \sim \mathcal{N}(0, \varsigma^2)$,则概率密度函数为 $f(w') \propto e^{- \|w'\|^2 / (2 \varsigma^2)}$
可以计算出后验概率为
$$f_{W|X,Y}(w) = \frac{f_{Y| X, W}(y)f(w')}{f_{Y|X}(y)}$$后验概率的对数形式2为
$$ \begin{align*} \ln f_{W|X,Y}(w) &= \ln f_{Y| X, W}(y) + \ln f(w') - \text{const} \\ & = -\text{const} \|Xw - y\|^2 - \text{const} \|w'\|^2 -\text{const} \end{align*} $$最大化后验概率,即最小化 $\|Xw - y\|^2 + \|w'\|^2$
最大似然估计:寻找参数 $w$,使得在该参数下,当前观测样本出现的概率最大
最大后验概率估计:寻找参数 $w$,使得在观察到当前样本的前提下,参数的后验概率最大
Ref: https://zhuanlan.zhihu.com/p/506449599
特征子集选择
添加特征会增加方差,但是不一定会降低偏差,通过去除难以预测的特征,可以降低偏差
最直接的方法是,我们可是使用 $d$ 个特征的 $2^d - 1$ 个特征子集,训练不同的模型,然后通过交叉检验选择最优的模型。但是计算开销过大
前向逐步选择:从 0 特征开始,每次加入一个最优的特征,直到验证集的误差开始升高。最优特征的选择,可以通过依次遍历不同的特征,并通过交叉检验获得。只需要训练 $O (d^2)$ 个模型,但是可能会错过组合在一起最优的多个特征
后向逐步选择:从 d 个特征开始,逐渐移除特征,每次选择可以使验证集性能下降最小的特征
LASSO
最小二乘线性回归 + $l_1$ 惩罚平均损失
LASSO 和岭回归一样,都是在最小二乘回归的基础上正则项,但是 LASSO 的 $l_1$ 会使某些维度的权重接近 0
寻找 $w$ 可以最小化 $\|Xw-y\|^2 + \lambda \|w'\|_1$,其中 $\|w'\|_1 = \sum_{i = 1}^d|w_i|$(不对常数项 $\alpha$ 惩罚)
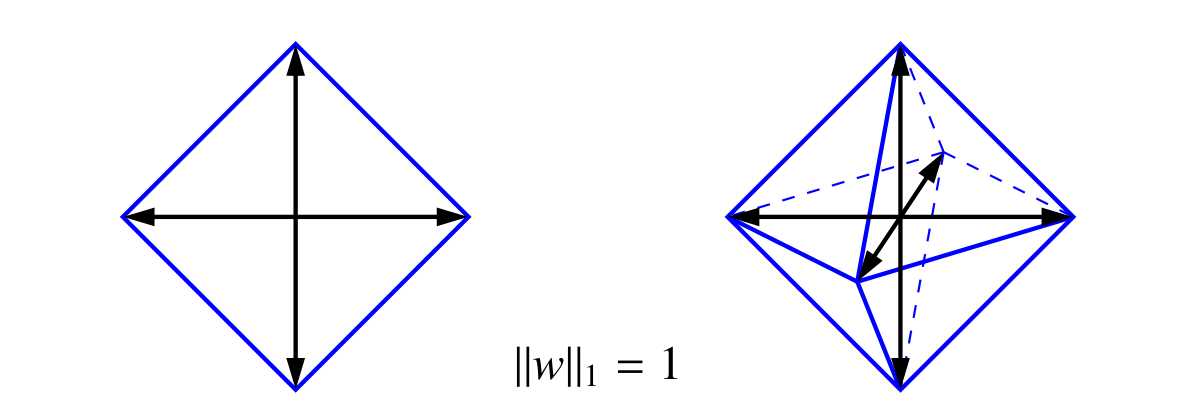
岭回归的正则项 $\|w'\|^2$ 是一个超球面,而 $\|w'\|_1$ 对应的是一个正多面体
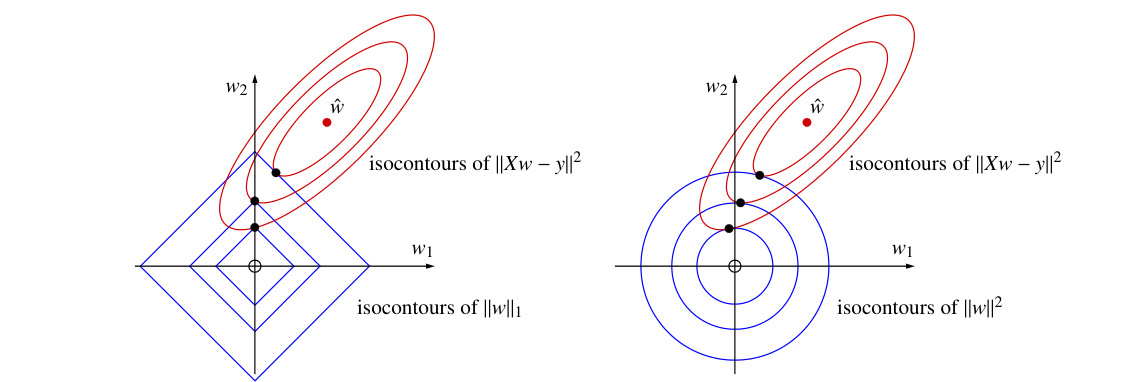
上图中,红色的椭圆形表示 $\|Xw - y\|^2$,其中最小二乘法的解为中心的红点。左边蓝色的四边形表示 $l_1$ 正则项,如果 $\lambda$ 较大,对应的四边形约小,两个图形的第一次相交于竖轴,此时特征 $w_1$ 对应的权重为 0,这种方法可以用于去除无用特征
