统计解释
一种典型的模型假设:
- 采样点来自一个未知的概率分布,即 $X_i \sim D$
- 标签 y 的值是一个未知的非随机函数 $g$ 的结果加上随机噪声,即
$\forall X_i, \quad y_i = g(X_i) + \varepsilon_i, \quad \varepsilon_i \sim D'$,其中 $D'$ 的均值为 0
回归问题的目标:找到一个映射 $h$ 来近似 $g$
理想的途径是,选择 $h(x) = E_Y[Y|X=x] = g(x) + E[\varepsilon] = g(x)$
从最大似然法推导最小平方代价函数
假设 $\varepsilon_i \sim \mathcal{N}(0, \sigma^2)$,那么 $y_i \sim \mathcal{N}(g(X_i), \sigma^2)$,那么 $y_i$ 的概率密度函数的对数形式为
$$\ln f(y_i) = -\frac{(y_i - g(X_i))^2}{2\sigma^2} - C$$其中 $C$ 表示一个常量
于是对数似然为
$$l(g;X,y) = \ln (f(y_1)f(y_2) \cdots f(y_n)) = -\frac{1}{2\sigma^2}\sum(y_i - g(X_i))^2 - C'$$从上式可以看出,最大化似然 $l (g; X, y)$,等价于选择一个函数 $g$,可以最小化 $\sum(y_i - g(X_i))^2$
经验风险
假设 $h$ 的风险是在联合概率分布 $(X, Y)$ 上的损失的期望,即 $R(h) = E[L]$
如果我们知道 $X$ 的分布,我们可以通过生成模型估计 $X$ 和 $Y$ 的联合概率分布。但是实际分布通常未知,只能假设所有的样本点都满足实际概率分布,然后最小化经验风险
$$\hat{R}(h) = \frac{1}{n} \sum_{i = 1}^n L(h(X_i), y_i)$$理论上,当样本数量 $n\rightarrow \infty$ 时,经验风险将会收敛到实际风险。通过最小化 $\hat{R}(h)$ 来选择 $h$ 的过程被称为经验风险最小化
从最大似然推导 logistic 损失
设样本点 $X_i$ 属于类别 C 的实际概率为 $y_i$,预测概率为 $h (X_i)$
假设总共有 $\beta$ 个和 $X_i$ 相同的数据点,那么将有 $y_i \beta$ 个属于类别 $C$,$(1-y_i)\beta$ 个不属于 $C$
那么似然为
$$\prod_{i = 1} ^n h(X_i)^{y_i \beta}(1 - h(X_i))^{(1 - y_i)\beta}$$对数似然为
$$ \begin{align*} l(h) & = \ln \mathcal{L}(h) \\ & = \beta \sum_i \underbrace{\left( y_i \ln h(X_i) + (1 - y_i) \ln (1 - h(X_i)) \right)}_{\text{logistic loss}} \end{align*} $$最大化似然,等价于最小化 logistic 损失之和
偏差-方差分解
偏差:由于 $h$ 无法完美拟合 $g$ 导致的误差
方差:由于拟合数据中的随机噪声造成的误差
由于训练数据 $X$ 和 $y$ 来自一个联合概率分布,我们用这些数据来选择一个权重,所以最终选择的拟合函数 $h$ 也来自一个概率分布
对风险进行分解($\gamma$ 和 $h(z)$ 互相独立)
$$ \begin{align*} R(h) &= E[L(h(z), \gamma)] \\ & = E[(h(z) - \gamma)^2] \\ & = E[h^2(z)] + E[\gamma^2] - 2 E[\gamma h(z)] \\ & = (Var(h(z)) + E[h(z)]^2) + (Var(\gamma) + E[\gamma]^2) - 2 E[\gamma]E[h(z)] \\ & = \underbrace{(E[h(z)] - E[\gamma])^2}_{偏差的平方} + \underbrace{Var(h(z))}_{方差} + \underbrace{Var(\varepsilon)}_{噪声} \end{align*} $$上式被称为风险函数的偏差-方差分解
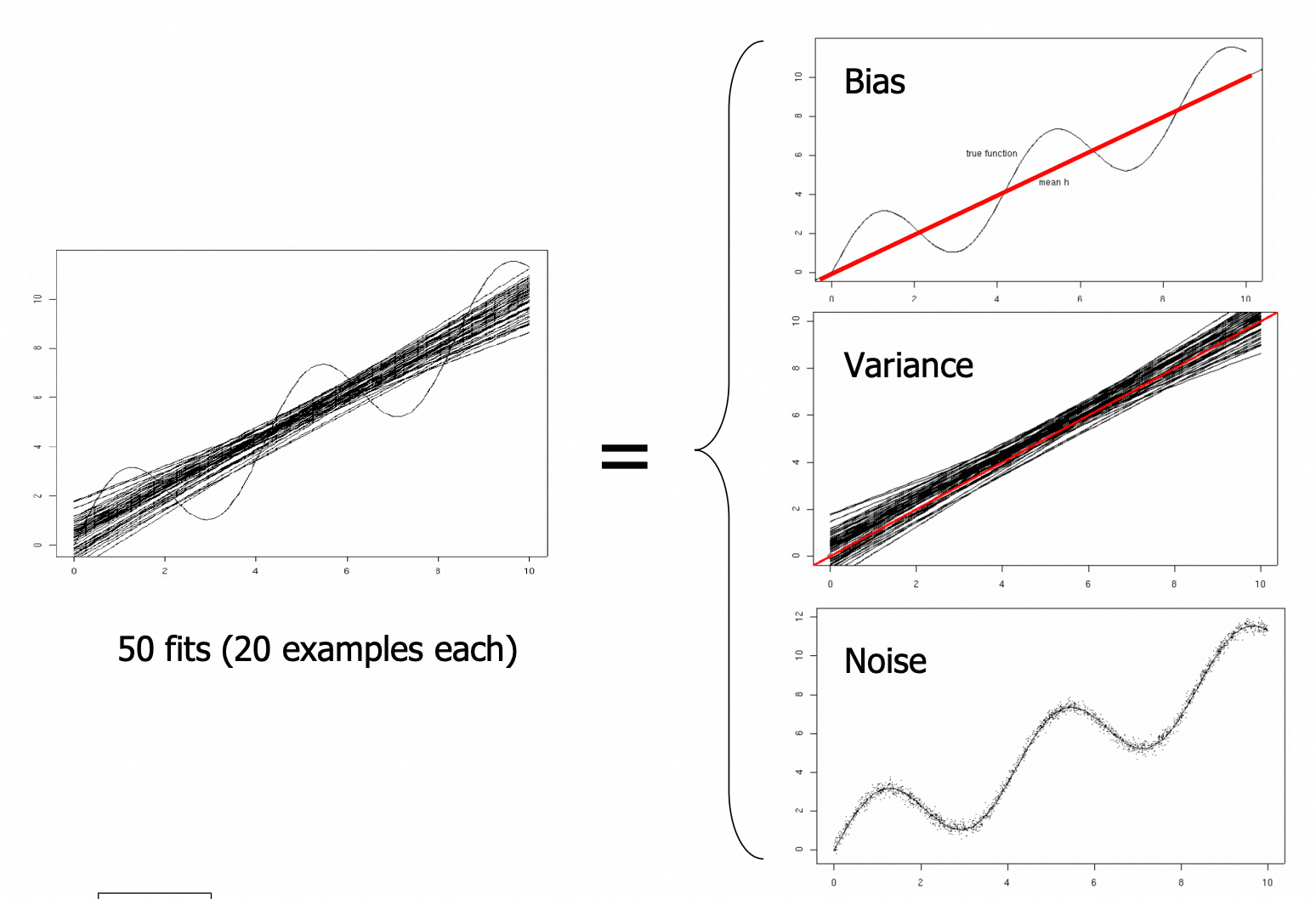
偏差-方差分解
上图中,左侧的 sine 曲线时实际函数 $g$,黑色直线是 50 条使用最小二乘线性回归拟合的结果 $h$,模型的风险可以分成右侧偏差、方差和噪声三个部分
基于偏差-方差分解,我们可以得到如下结论:
- 欠拟合意味着偏差过大
- 大多数情况下,过拟合是由于方差过大
- 训练误差一般反映偏差但是体现不出方差,但是测试误差可以体现两者
- 对于大多数分布来说,当训练数量量 $n\rightarrow \infty$ 时,方差趋近于 0
- 如果 $h$ 可以很好地拟合 $g$,那么对于大多数分布而言,当训练数量量 $n\rightarrow \infty$ 时,偏差趋近于 0
- 如果 $h$ 不能很好地拟合 $g$,那么对于大多数样本点,偏差较大
- 添加一个好的特征可以降低偏差,但是添加一个坏的特征很少会增加偏差
- 添加特征通常会增加偏差
- 噪声误差无法去除
- 在测试集中,噪声只影响 $Var (\varepsilon)$;在训练集中,噪声同时影响偏差和方差
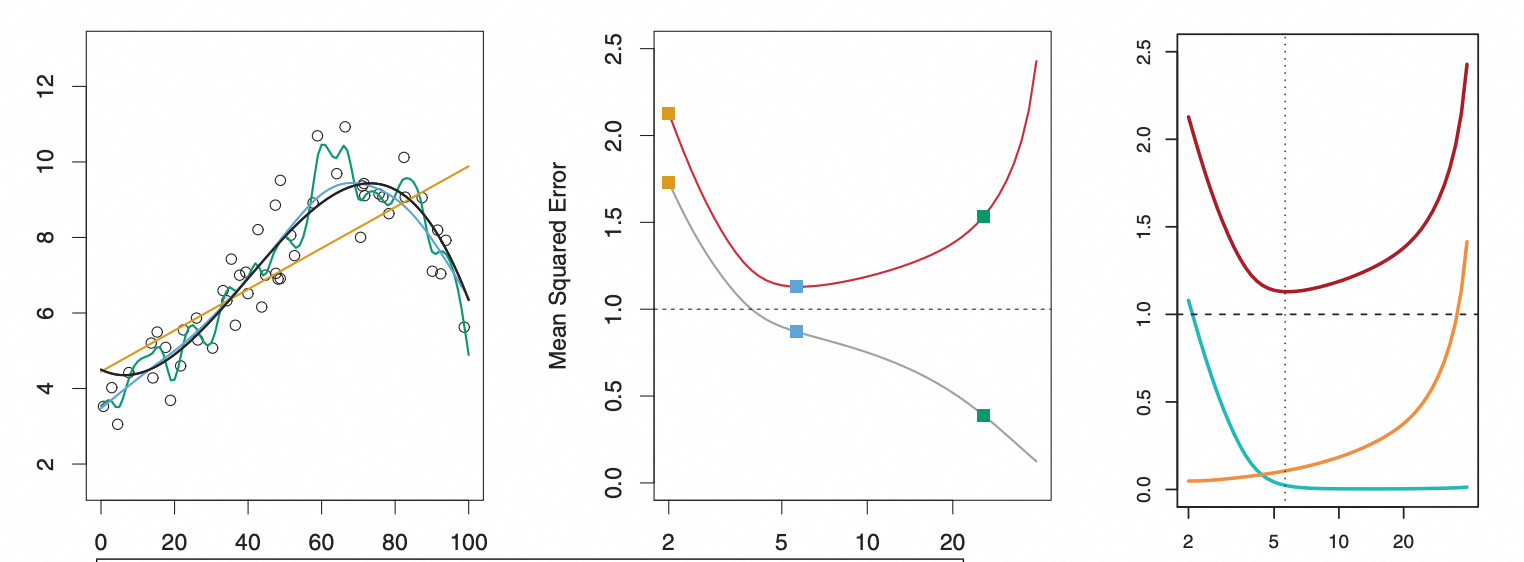
左图中黑色线条为真实的函数,所有点在真实的分布上添加噪声采样而得,不同颜色的曲线分别是使用不同阶数拟合数据得到的曲线。中间灰色的曲线表示训练误差随模型阶数变化的曲线,红色的是测试误差随训练阶数变化的曲线。右边红色曲线是测试集上的平方误差(包含了偏差和方差)随结束变化的曲线,绿色的表示偏差,红色的表示方差
