最小二乘多项式回归
我们可以使用一个非线性的多项式特征 $\Phi(X_i)$ 来替代 $X_i$,例如
$$\Phi(X_i) = \begin{bmatrix}X_{i1}^2 & X_{i1}X_{i2} & X_{i2}^2 & X_{i1} & X_{i2} & 1\end{bmatrix}$$一旦我们创建了多项式特征向量,接下来的流程将和线性回归或 logistic 回归一致
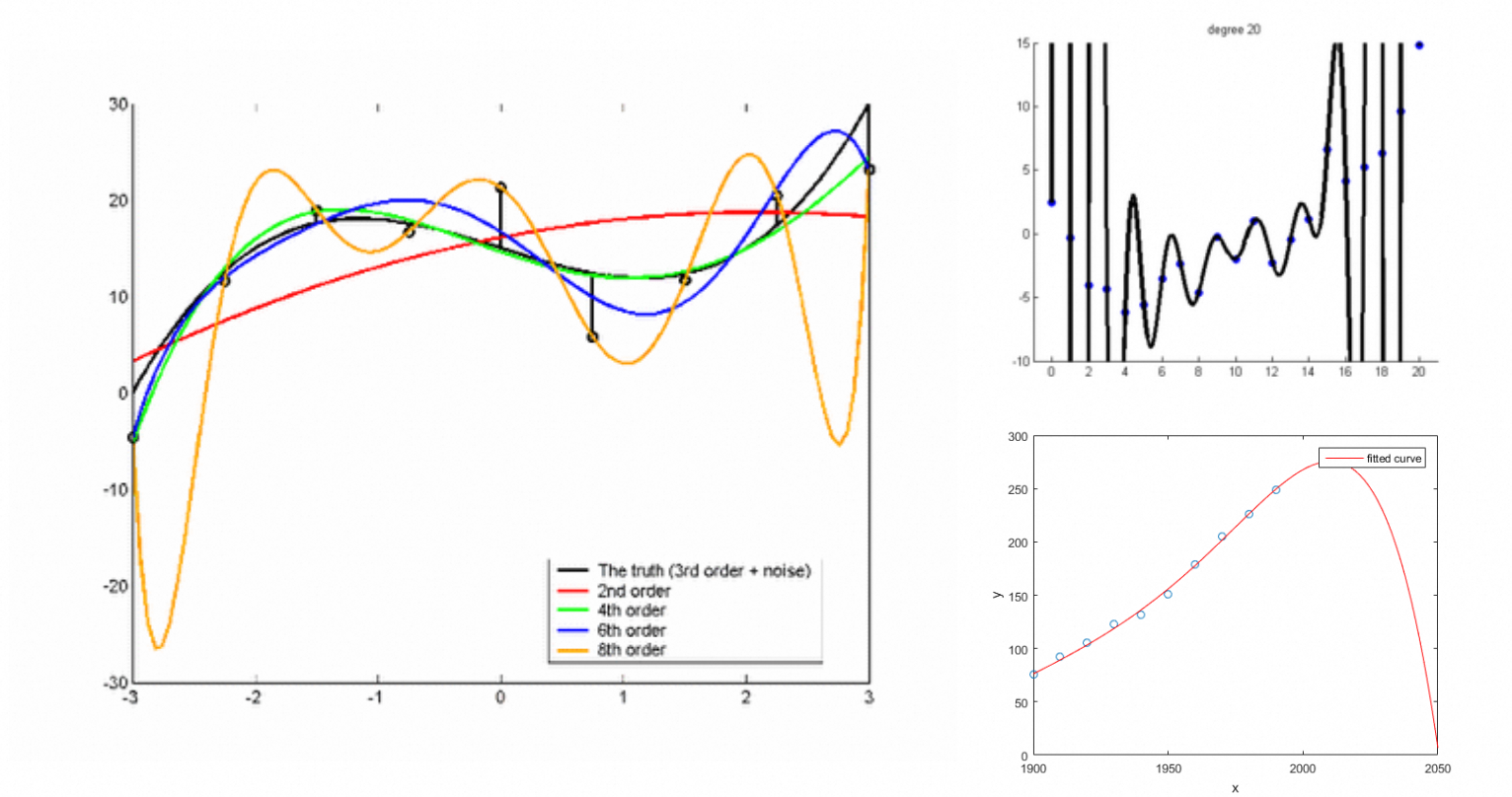
不同次数的拟合效果
如果多项式的次数过大,非常容易过拟合
加权最小二乘回归
如果某些样本点比其他的样本更加可信,或者有些样本点我们希望更好地拟合,那么我们可以对这些点施加更高的权重,而对异常点施加更低的权重
为每个样本点设定一个权重 $\omega_i$,$n$ 个权重组成一个对角矩阵 $\Omega$。于是加权的条件下问题描述变成:
寻找一个 $w$ 使得可以最小化 $(Xw - y)^T \Omega (Xw - y) = \sum_{i = 1}^n \omega_i (X_i \cdot w - y_i)^2$
同样,我们可以通过计算梯度为 0 的点求解 $w$,即 $X^T\Omega X w = X^T \Omega y$
牛顿法
牛顿法是一种迭代寻找函数 $J(w)$ 的最优解的方法($J(w)$ 必须是光滑的),通常比梯度下降更快
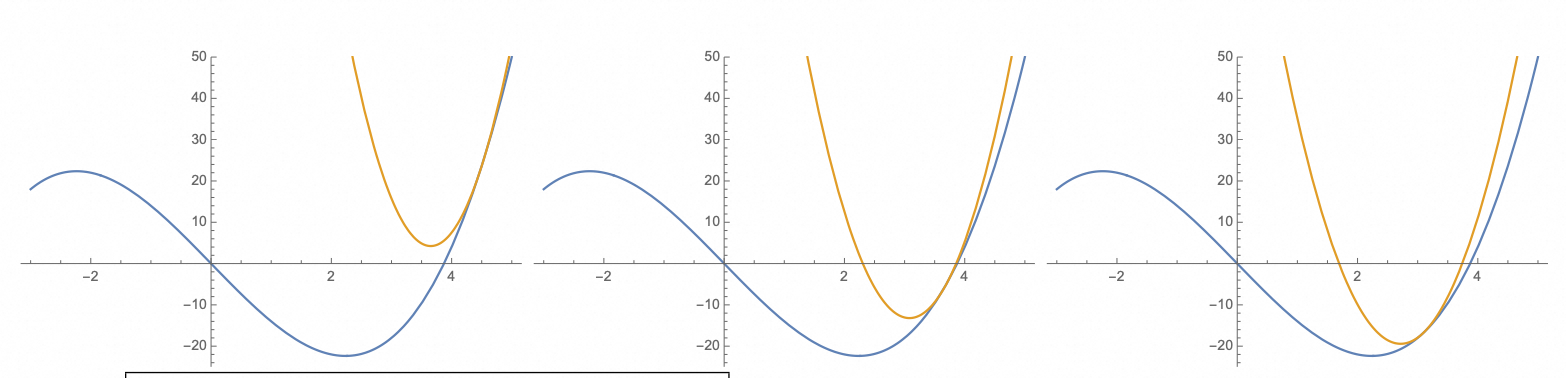
牛顿法的迭代过程
牛顿法的核心是通过二次函数(抛物线)来局部逼近最优解,每次都移动到抛物线的顶点(上图中棕色曲线是用于近似的二次曲线,从左到右棕色曲线的顶点逐渐逼近最优点):
- 给定一个点 $v$,使用二次函数在 $v$ 附近近似 $J(w)$
- 跳转到二次函数的顶点
- 重复上述步骤直到到达停止条件
在每一次迭代中寻找顶点的方式如下:
以 $v$ 为基准,在 $w$ 处梯度的泰勒展开为
其中 $\nabla^2 J(v)$ 是Hessian 矩阵,通过计算梯度为 0 的点得到顶点
$$w \approx v - (\nabla^2 J(v))^{-1} \nabla J(v)$$上式中存在计算矩阵的逆的过程,直接计算矩阵的逆通常计算量非常大并且不稳定,一般将其转换为一个线性方程组求解,即 $(\nabla^2 J(w))e = - \nabla j(w)$
牛顿法的算法流程可以表述如下:
$$ \begin{align*} & \text{pick starting point } w \\ & \text{repeat until convergence} \\ & \quad e \leftarrow \text{ solution to liner system } (\nabla^2 J(w))e = - \nabla j(w) \\ & \quad w \leftarrow w + e \end{align*} $$牛顿法无法区分最小值点、最大值点和鞍点,所以初始点需要足够接近目标点
如果目标函数是一个二次函数,牛顿法只需要一步就可以找到精确解,$J$ 越接近二次函数,牛顿法越快收敛
对于某些优化问题,牛顿法相比梯度下降可以更快收敛。首先,牛顿法会寻找到达最小值的正确步长,而不是任意距离;其次,牛顿法会尝试寻找最优的下降方向,而不是梯度最陡的方向
然而,牛顿法也有一些缺点。牛顿法需要计算 Hessian 矩阵,在维度较高的时候计算开销非常大,所以神经网络一般不使用牛顿法。此外,牛顿法要求目标函数必须光滑,例如感知机的风险函数就无法使用牛顿法
使用牛顿法优化 Logistic 回归
10 回归I:最小二乘回归和逻辑回归中已经计算了 $\nabla J(w) = - X^T (y - s)$ ,可以进一步计算牛顿法需要的二阶梯度(Hessian 矩阵)
$$\nabla_w^2 J(w) = \sum_{i = 1} ^ n s_i (1 - s_i) X_i X_i^T = X^T \Omega X$$其中
$$ \Omega = \begin{bmatrix} s_1(1 - s_1) & 0 & \dots & 0 \\ 0 & s_2(1 - s_2) & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \dots & s_n(1 - s_n) \end{bmatrix} $$$s_i \in (0,1)$ (logistic 函数的输出),所以 $\Omega$ 对于任意 $w$ 是正定的
$\Rightarrow$ Hessian 矩阵 $\nabla_w^2 J(w) =X^T \Omega X$ 是半正定的
$\Rightarrow$ 函数 $J$ 是凸函数 (二阶导数大于等于零,Hessian 矩阵半正定)
由于 logistic 函数的代价函数 $J (w)$ 是凸的,所以如果可以收敛的话,牛顿法可以找到全局最优点
logistic 回归的牛顿法优化可以表示成:
$$ \begin{align*} & w \leftarrow 0 \\ & \text{repeat until convergence} \\ & \quad e \leftarrow \text{solution to normal equations} (X^T\Omega X) e = X^T (y - s) \\ & \quad w \leftarrow w + e \end{align*} $$牛顿法优化 logistic 回归是,$e$ 受远离决策边界且被分类错误的点影响最大($y_i - s_i$ 最大),受远离决策边界且被分类正确的点影响最小($y_i - s_i$ 最小)
如果数据集非常大,为了加快训练,开始可以失效所以样本点的子集(初期的更新比较粗略),随着迭代进行逐渐增大子集的大小(后期需要精细的参数更新)
LDA 和 logistic 回归对比
LDA 的优点:
- 对于可以很好分离的类别,LDA 很稳定,而 logistic 回归不稳定
- 对于大于 2 个类别的情况,LDA 仍然简洁,而 logistic 回归需要改为 softmax 回归
- LDA 一般对于样本符合高斯分布的情况表现更好,特别是样本量 $n$ 较小的情况
logistic 回归的优点:
- logistic 回归更加强调决策边界 logistic 回归对于距离边界不同距离的点施加的权重不同,而 LDA 会一视同仁。所以 logistic 回归能够更好地降低训练损失,但是对异常数据更敏感
- logistic 回归对非高斯数据的鲁棒性更好
ROC 曲线
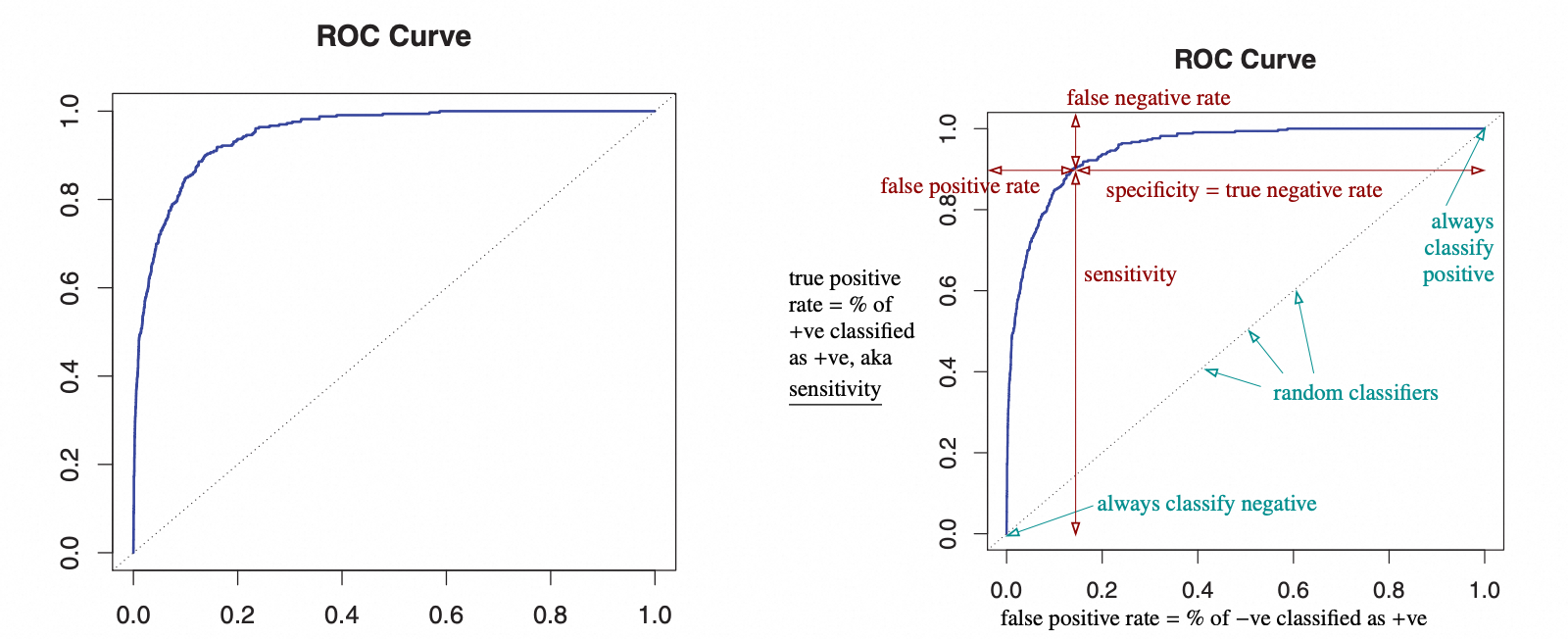
ROC曲线
ROC 曲线展示了在不同的判别门限设置下,假阳性和真阳性的比例变化的曲线,ROC 曲线可以通过在不同的判别门限下测试得到
- x 轴表示假阳性(负类别别判别成正类别)的比例
- y 轴表示真阳性的比例
- 曲线到顶部的垂直距离表示假阴性的比例
- 曲线到右边的水平距离表示真阴性的比例
右上角的点表示永远被判别为正例,左下角的点表示永远被判别为负例,对角线表示一个随机分类器
通过计算 ROC 曲面下的面积可以衡量一个分类器的好坏,面积为 1 表示分类器永远可以正确分类,面积为 0.5 表示一个随机分类器
