回归问题
- 分类问题:给定样本点 $x$,预测类别
- 回归问题:给定样本点 $x$,预测数值
QDA和LDA不仅仅估计了一个分类器,它们也可以给出估计正确的概率,所以QDA和LDA是对概率的回归
回归问题的拟合可以分成两个部分:
- 选择一个回归函数 $h(x;w)$,其中参数为 $w$
- 选择一个优化的代价函数(通常基于损失函数定义)1
一些回归函数:
(1) 线性:$h(x;w,\alpha)=w\cdot x + \alpha$
(2) 多项式型
(3) logistic2:$h(x;w,\alpha)=s(w\cdot x + \alpha)$,其中 $s$ 是logistic函数 $s(\gamma)=\frac{1}{1+e^{-\gamma}}$
一些损失函数:
(A) 平方误差:$L(\hat{y}, y) = (\hat{y} - y)^2$
(B) 绝对值误差:$L(\hat{y}, y) = |\hat{y} - y|$
(C) logistic损失(交叉熵):$L(\hat{y}, y) = -y \ln \hat{y} - (1 - y) \ln (1 - \hat{y})$
一些代价函数:
(a) 平均:$J(h) = \frac{1}{n} \sum_{i = 1}^n L(h(X_i), y_i)$
(b) 最大:$J(h) = \max_{i=1}^n L(h(X_i), y_i)$
(c) 加权:$J(h) = \sum_{i = 1}^n w_i L(h(X_i), y_i)$
(d) $l_2$ 正则化:$J + \lambda \|w\|_2^2$
(e) $l_1$ 正则化:$J + \lambda \|w\|_1$
上述不同的回归和损失与代价函数的选择,可以组成不同的算法:
- 最小二乘回归(Least-squares linear regression):(1) + (A) + (a),成本函数是二次的,可以通过微积分直接求解
- 岭回归(Ridge regression):(1) + (A) + (a) + (d),成本函数是二次的,可以通过微积分直接求解,$l_2$ 范数限制权重不过大防止过拟合
- Lasso:(1) + (A) + (a) + (e),二次规划问题,$l_1$ 正则化倾向于某些权重变为0,适合特征较多时的特征选择
- 逻辑回归(logistic regression):(3) + (C) + (a),成本函数是凸函数,可以通过梯度下降法求解
- 最小绝对偏差(least absolute deviations):(1) + (B) + (a),线性规划,绝对误差对离群点不那么敏感
最小二乘回归
线性回归函数 + 平方损失 + 平均代价
问题描述:寻找$w$,$\alpha$使得$\sum_{i = 1}^n (X_i \cdot w + \alpha - y_i)^2$最小。如果将偏置$\alpha$包含在权重$w$中,使$w$为一个$d+1$维的向量,那么上述优化问题可以表述成最小化$RSS(w) = \| X w - y \|^2$
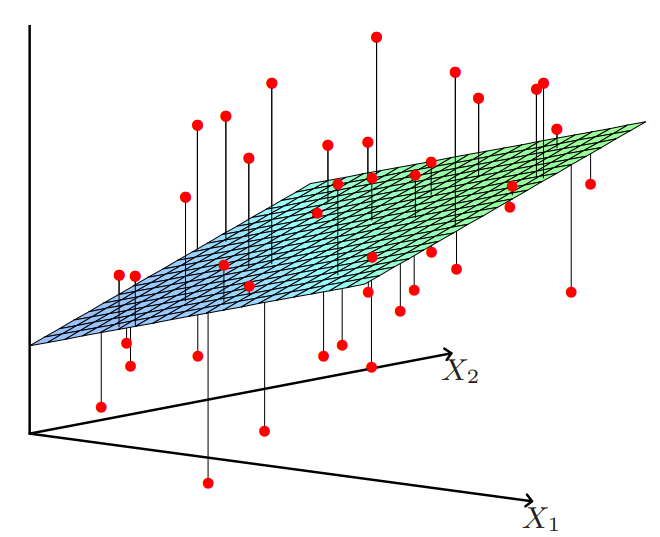
$RSS(w)$为凸函数,在导数为$0$达到最小值,即$2X^TXw - 2X^T y = 0$,解得$w = (X^T X)^{-1} X^T y$
上式包含一个假设,即$X^T X$是非奇异的(如果某些样本点共线或者共面),反之解不唯一或不存在
可以看出$((X^T X)^{-1} X^T)X=I$,所以$X^+ = (X^T X)^{-1} X^T$被称为矩阵$X$的伪逆
将$w$的解代入可得$y=X(X^T X)^{-1} X^T y = Hy$,其中矩阵$H$被称为帽子矩阵(hat matrix)
- 优点:容易计算,有唯一、稳定的解
- 缺点:对异常值敏感,因为误差被平方;如果$X^T X$是奇异的则无法适用
逻辑回归
logistic 函数 + logistic 损失 + 平均代价
拟合概率,通常被用于分类问题,标签$y_i$可以为任意概率值,但是通常为$0$或$1$
QDA和LDA是生成模型,而逻辑回归时判别模型
问题描述:寻找$w$使其可以最小化代价函数
$$ J = \sum_{i = 1} ^n L(s(X_i \cdot w), y_i) = -\sum_{i = 1}^n \left( y_i \ln s(X_i \cdot w) + (1 - y_i) \ln(1 - s(X_i \cdot w)) \right) $$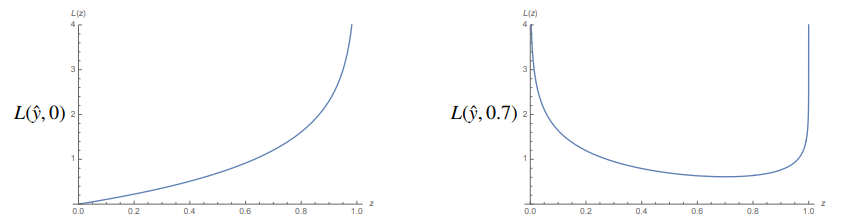
可以看出,在预测概率$\hat{y}$和真实概率相同的条件下,logistics损失达到最小值
逻辑回归的代价函数$J(w)$是凸的,可以通过梯度下降法求解
logistic函数的导数为
$$ s'(\gamma) = \frac{\mathrm{d}}{\mathrm{d}\gamma} \frac{1}{1 + e^{-\gamma}} = \frac{e^{-\gamma}}{(1 + e^{-\gamma})^2} = s(\gamma)(1 - s(\gamma)) $$$J(w)$管于$w$的梯度为
$$ \begin{aligned} \nabla_w J &= - \sum \left( \frac{y_i}{s_i} \nabla s_i - \frac{1 - y_i}{1 - s_i} \nabla s_i \right) \\ &= - \sum \left( \frac{y_i}{s_i} - \frac{1 - y_i}{1 - s_i} \right) s_i (1 - s_i) X_i \\ &= - \sum(y_i - s_i) X_i \\ &= -X^T (y - s) \end{aligned} $$其中$s = \begin{bmatrix} s_1 \\ s_2 \\ \vdots \\ s_n \end{bmatrix}$是$n$个估计值组成的向量
于是梯度下降的准则为
$$ w \leftarrow w + \varepsilon X^T (y - s) $$对于线性可分数据,逻辑回归的梯度下降法虽然能保证找到一个完美的分类边界,并且这个边界最终会是理论上最优的最大间隔,但其权重会趋于无穷大,且收敛速度极慢
