机器学习 09 高斯判别分析（各向异性）

我们已经定义了多维正态分布

$$ f(x)=n(q(x)),\quad n(q) = \frac{1}{\sqrt{(2\pi)^d|\Sigma|}}e^{-q/2},\quad q(x)=(x-\mu)^T \Sigma^{-1} (x-\mu) $$

其中有三个重要的矩阵：

$\Sigma = V\Gamma V^T$ 是协方差矩阵，其中它的特征值是沿着对应的特征向量方向的方差，即 $Var(v_n^TX)=\lambda_n$
$\Sigma^{1/2}=V\Gamma^{1/2}V^T$ 将球面映射到椭球面，它的特征值是椭球面的半轴长
$\Sigma^{-1}=V\Gamma^{-1}V^T$ 是精度矩阵，它的二次型决定了曲面的形状

各向异性高斯的参数的最大似然参数估计

给定训练样本 $X_1, \dots, X_n$ 和类别 $y_1, \dots, y_n$，我们期望拟合一个最优的高斯分布，使得每个样本点都能归属到对应的类别

首先估计出先验概率 $\hat{\pi}_C = a / n$，均值 $\hat{\mu}_C = \frac{1}{n} \sum_{i = 1}^n X_i$

对于 QDA，可以估计出条件协方差

$$\hat{\Sigma}_C = \frac{1}{n_C} \sum_{i:y_i = C} (X_i - \hat{\mu}_C)(X_i - \hat{\mu}_C)^T$$

其中 $\hat{\Sigma}_C$ 是一个半正定矩阵，如果它有零特征值，那么不存在逆矩阵 $\hat{\Sigma}_C^{-1}$，并且行列式 $| \hat{\Sigma}_C|=0$，QDA 将会失效，可以通过降维解决

对于 LDA，所有类别的协方差相同

$$ \hat{\Sigma} = \frac{1}{n} \sum_{C} \sum_{i:y_i = C} (X_i - \hat{\mu}_C)(X_i - \hat{\mu}_C)^T $$

QDA

选定类别 $C$ 使得 $P(Y=C|X=x)$ 最大，其实就是选定 $C$ 最大化二次判别函数

$$ \begin{align*} Q_C(x) &= \ln \left( (\sqrt{2\pi})^d f_{X|Y=C}(x) \pi_C \right) \\ &= -\frac{1}{2} (x - \mu_C)^T \Sigma_C^{-1} (x - \mu_C) - \frac{1}{2} \ln |\Sigma_C | + \ln \pi_C \end{align*} $$

在多类别的条件下，只需要选择最大的判别函数对应的类别

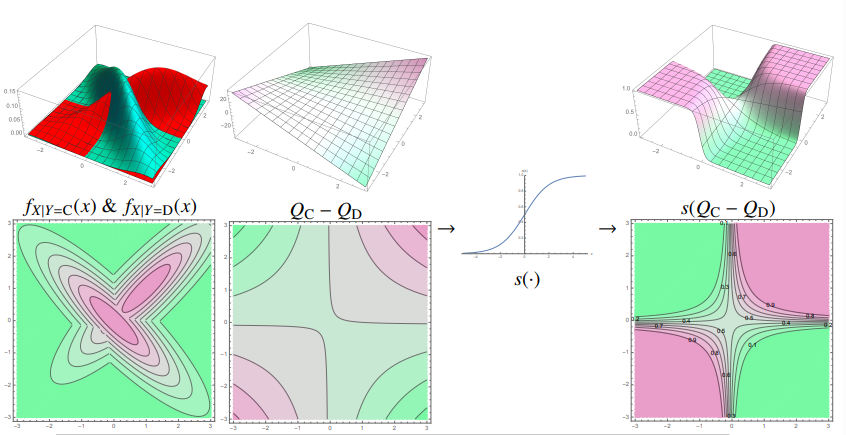
上图中，在两个类别的场景下

左图是两个类别的$C$和$D$的条件概率分布

中间的决策函数 $Q_C(x) - Q_D(x)$ 是一个二次函数，所以决策边界是一个二次曲面
右图中是后验概率$P(Y=C | X= x) = s(Q_C(x) - Q_D(x))$

如果我们准确已知真实的参数$\pi_C$，$\mu_C$和$\Sigma_C$，我们可以直接得到贝叶斯分类器和贝叶斯最优决策边界；如果我们只能从数据中估计$\hat{\pi}_C$，$\hat{\mu}_C$和$\hat{\Sigma}_C$，这个过程就是QDA算法，QDA分类器只能逼近贝叶斯分类器

LDA

如果所有类别的协方差$\Sigma$相同，决策函数中的二次项互相抵消，决策边界是一个线性超平面

$$ Q_C(x) - Q_D(x) =\underbrace{ (\mu_C - \mu_D)^T \Sigma^{-1} x }_{w^T x} \underbrace{ - \frac{\mu_C^T \Sigma^{-1} x - \mu_D^T \Sigma^{-1} \mu_D}{2} + \ln\pi_C -\ln\pi_D}_{+\alpha} $$

其中决策边界为$w^T x + \alpha = 0$

后验概率为$P(Y = C | X = x) = s(w^T x + \alpha)$

多类别LDA的情况：选择使线性判别函数最大的类别$C$，判别函数的定义为

$$ \mu_C^T \Sigma^{-1} x - \frac{\mu_C^T \Sigma^{-1} \mu_C}{2} + \ln \pi_C $$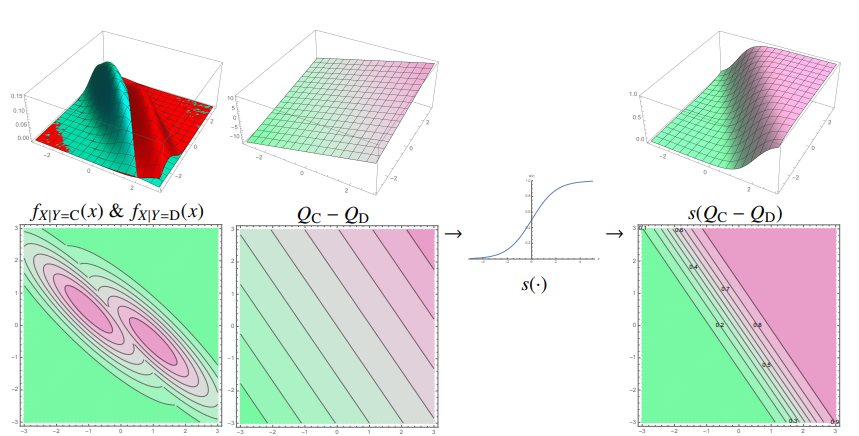

QDA和LDA的对比

在两个类别的条件下，虽然我们估计了高斯分布地较多参数，但是在决策函数$Q_C(x) - Q_D(x)$中

LDA有$d+1$个参数（包括$w$的$d$个参数和$\alpha$的1个参数），所以LDA更加容易欠拟合
QDA有$\frac{d(d+3)}{2}+1$个参数¹，所以QDA更加容易过拟合

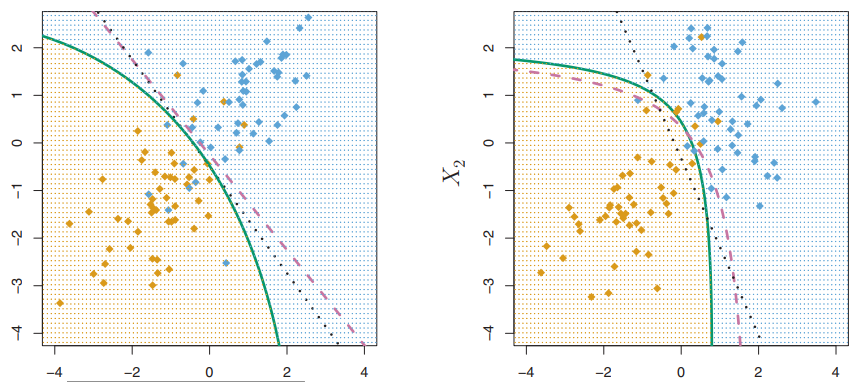
在上图中，贝叶斯决策边界是紫色的虚线，QDA决策边界是绿色的实线，LDA的决策边界是黑色的点线。当贝叶斯决策边界是线性的时，LDA可以得到更加稳定的拟合，而QDA可能过拟合；当贝叶斯决策边界是曲线时，QDA可能得到更好的拟合效果

改变先验概率$\pi$或者损失，等价于对决策函数施加额外的常数偏置²

在二分类的情况下，选择$p$的决策阈值，等价于选择$\pi_C=1-p，\pi_D=p$；或者选定非对称损失，假阳性损失为$p$，假阴性损失为$1-p$

一些额外的术语

假设$X$是一个$n\times d$的设计矩阵（design matrix），它的每一行是一个$d$维的样本点$X_i^T$

对$X$进行中心化：从$X$的每一行减去$\hat{\mu}^T$，得到$\dot{X}$，其中$\hat{\mu}^T$是X的所有行的平均，所以$\dot{X}$的所有行的均值为0
此时可以计算出所有样本点的协方差$\text{Var}(R)=\frac{1}{n}\dot{X}^T\dot{X}$
对$\dot{X}$去相关：对$\dot{X}$进行旋转，即$Z=\dot{X}V$，其中$\text{Var}(R)=V\Lambda V^T$
上式通过旋转将样本点转换到了特征向量对应的坐标系³，此时特征向量就是坐标轴，所以$\text{Var}(Z)=\Lambda$，数据点在不同坐标轴方向的相关性为0
对$\dot{X}$球化：$W=\dot{X} \text{Var}(R)^{-1/2}$⁴
对$X$白化：中心化+球化，$X \rightarrow \dot{X} \rightarrow W$

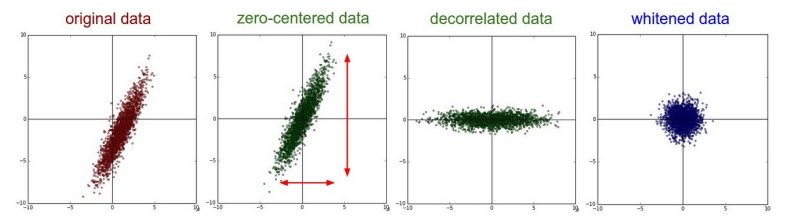
白化被应用到很多机器学习算法，例如支持向量机和神经网络。某些特征的数值可能远大于其他特征，例如它们的测量单位不同。SVM 对由数值大的特征的惩罚，会比对数值小的特征更重

QDA的决策函数$Q_C(x) - Q_D(x)=x^T \underbrace{(\Sigma_D^{-1} - \Sigma_C^{-1})}_{d(d-1) / 2 \text{ params}}x + \underbrace{(\mu_C^T \Sigma_C^{-1} - \mu_D^T \Sigma_D^{-1})}_{d \text{ params}} x + \underbrace{\dots}_{1 \text{ params}}$ ↩︎
贝叶斯决策规则：$\text{if } L(-1,1)P(Y=1|X=x) > L(1, -1)P(Y=-1|X=x) \text{ then } r^*(x) = 1$ ↩︎
矩阵$V$是一个由特征向量组成的正交矩阵，用它乘原数据，相当于将原坐标变换到这些特征向量对应的新坐标系 ↩︎
$\Sigma^{1/2}$将球面映射到椭球面 ↩︎