机器学习 08 特征向量和多维正态分布

特征向量

给定一个方阵 $A$，如果存在一个向量 $v \neq 0$ 和常量 $\lambda$，满足 $Av = \lambda v$，那么 $v$ 是 $A$ 的一个特征向量，$\lambda$ 是与其对应的 $A$ 的特征值

特征向量乘以 $A$ 后，仍然指向相同的或者相反的方向

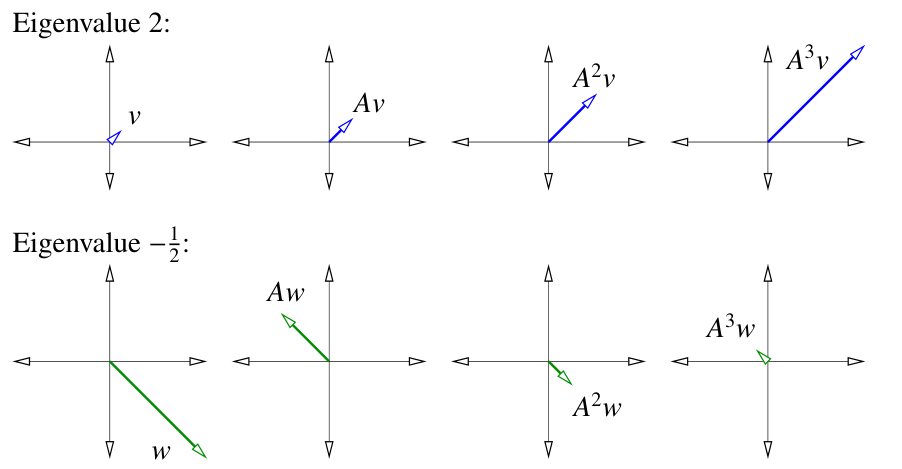
定理：如果 $v$ 是 $A$ 的特征向量，并且其对应的特征值为 $\lambda$，那么 $v$ 也是 $A^k$ 的特征向量，对应的特征值为 $\lambda^k$

谱定理（Spectral Theorem）：每个 $n \times n$ 维的实对称矩阵有 $n$ 个实数特征值和 $n$ 个特征向量，并且不同特征值的特征向量之间正交

使用特定的特征向量构建矩阵

选定 n 个互相正交的单位向量 $v_1,\dots,v_n$，那么矩阵 $V=\begin{bmatrix}v_1 & v_2 & \cdots & v_n\end{bmatrix}$ 满足 $V^TV=VV^TI$，$V$ 是一个正交矩阵

正交矩阵乘一个向量，不会改变向量的长度；正交矩阵同乘两个向量，不会改变两个向量之间的夹角

选定特征值构成对角矩阵

$$ \Lambda = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix} $$

根据特征向量的定义，有：$AV=V\Lambda$

两侧同乘 $V^T$ 可得

$$A=V\Lambda V^T = \sum_{i=1}^n \lambda_iv_iv_i^T$$

上式即为矩阵的特征分解

如果已知一个对称概率密度矩阵 $\Sigma$，我们可以通过以下方式得到它的平方根 $A=\Sigma^{1/2}$：

计算 $\Sigma$ 的特征向量和特征值
计算 $\Sigma$ 的特征值的平方根
使用 $\Sigma$ 的特征向量和特征值的平方根构造矩阵 $A$

二次型 Quadratic Form

矩阵 $M$ 的二次型为 $x^T M x$

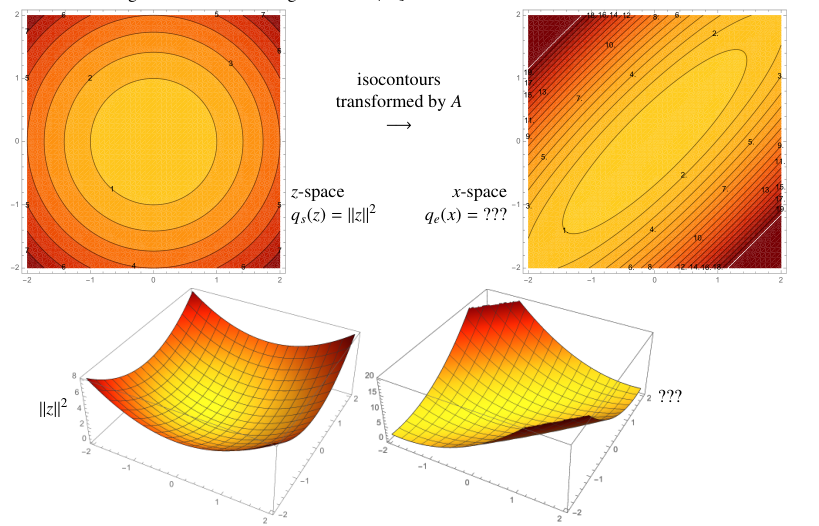
假设我们已知一个二次型 $q_s(z)=z^TIz =\|z\|^2$ ，它的等值线为圆形如上图左边
我们有一个变化矩阵

$$ A = V\Lambda V^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & -\frac{1}{2} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} $$

通过变换 $z = Ax$ 将 $z-$ 空间中的圆形等高线变为上图右边 $x-$ 空间中的椭圆等高线 $q_e(x)$。在等高线 $q_e(x)$ 中，$(1,1)$ 被放大 2 倍，$(1, -1)$ 方向被收缩 -1/2 倍

可以求出等高线的表达式

$$q_e(x) = q_s(A^{-1}x) = \|A^{-1}x\|^2=x^TA^{-2}x$$

可知二次方程 $x^TA^{-2}x$ 的等高线是一个由 $A$ 的特征向量和特征值决定的椭圆

同理可得，$\{x:x^TA^{-2}x=1\}$ 是一个椭球体，它的轴线是 $v_1,v_2,\dots,v_n$，半轴径是 $\lambda_1,\lambda_2,\dots,\lambda_n$（$\|Av_n\|=\lambda_n$）

所以我们可以知道，矩阵 $M$ 的二次型 $x^TMx$ 的等高面是一个由 $M^{-1/2}$ 的特征向量和特征值决定的椭球面
特殊情况：如果 $M$ 是对角矩阵，那么特征向量就是坐标轴，及椭球面的轴线和坐标轴平行

已知一个对称矩阵 $M$，那么

如果 $w^TMw>0$ 对于所有的 $w\neq0$ 都成立，那么 $M$ 是正定矩阵（positive definite matrix），所有特征值都是正数；
如果 $w^TMw\ge0$ 对于所有的 $w\neq0$ 都成立，那么 $M$ 是半正定矩阵（positive semi-definite matrix），所有特征值都是非负数；
如果 $w^TMw\le0$ 对于所有的 $w\neq0$ 都成立，那么 $M$ 是半负定矩阵（negative semi-definite matrix），所有特征值都是非正数；
如果既不是半正定矩阵又不是半负定矩阵，则 $M$ 是不定矩阵（indefinite matrix）

可逆矩阵$\Leftrightarrow$ 行列式不为 0 $\Leftrightarrow$ 没有 0 特征值

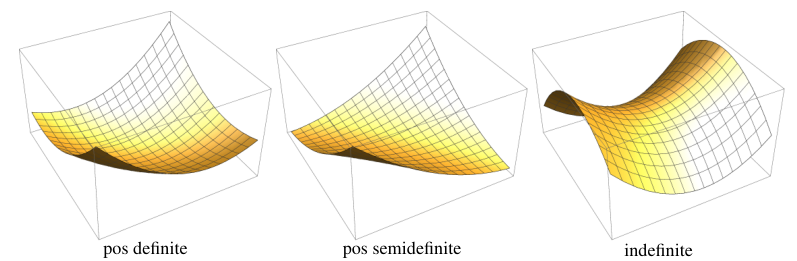
对于正定矩阵，它在所有方向上束缚住了曲面，形成了一个封闭的椭球面；而半正定矩阵在某些方向松开，使得曲面可以在这些方向无限延生，形成了柱面；如果不是正定矩阵，则为双曲面

各向异性高斯 Anisotropic Gaussians

对于一个多维高斯分布 $X\sim \mathcal{N}(\mu,\Sigma)$，$X$ 和 $\mu$ 是一个 $d$ 维向量，如果在不同的方向有不同的方差，概率密度函数可以表示为

$$f(x) = \frac{1}{\sqrt{(2\pi)^d|\Sigma|}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$$

其中 $\Sigma$ 是一个半正定矩阵，被称为协方差矩阵；$\Sigma^{-1}$ 也是半正定矩阵，被称为精度矩阵（precision matrix）

如果把概率密度函数写成 $f(x)=n(q(x))$，其中 $q(x)=(x-\mu)^T\Sigma^{-1}(x-\mu)$
$q(x)$ 是一个中心在 $\mu$ 的柱面，由精度矩阵 $\Sigma^{-1}$ 决定；$n(\cdot)$ 是一个单调凸函数，不会改变等值面的形状（只改变数值，不改变性质和位置，如下图）

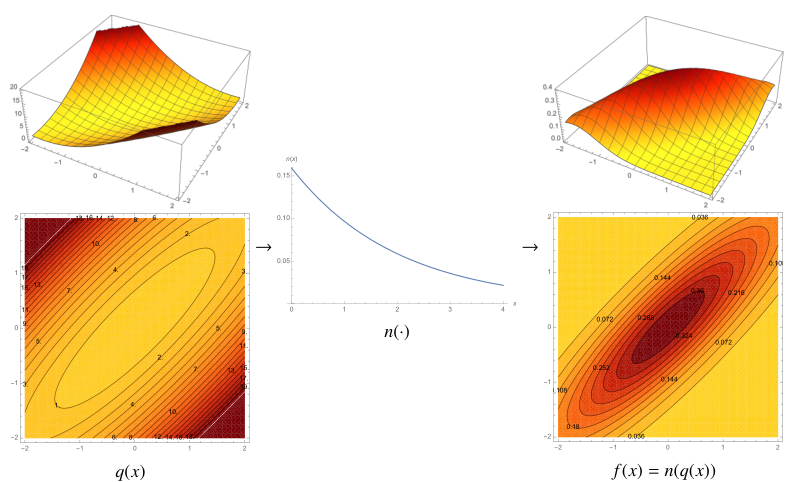
对于高斯随机过程的概率密度函数来说，对应的等值面和 $q(x)=(x-\mu)^T\Sigma^{-1}(x-\mu)$ 相同，只是经过了数值缩放。它在均值 $\mu$ 处到达最大值，在远离 $\mu$ 处逐渐趋近于零

$q(x)$ 也等于 $\Sigma^{-1 / 2}x$ 到 $\Sigma^{-1 / 2}\mu$ 的距离的平方，即

$$d(x, \mu) = \|\Sigma^{-1 / 2}x - \Sigma^{-1 / 2}\mu\| = \sqrt{(x- \mu)^T \Sigma^{-1} (x - \mu)} = \sqrt{q(x)}$$

协方差

假设 $R, S$ 是随机变量，可以是列向量或者常量，那么
协方差 $Cov(R, S) = E[(R- E[R])(S - E[S])^T]=E[RS^T] - \mu_R \mu_S^T$
方差 $Var(R) = Cov(R, R)$

如果 $R$ 是一个向量，那么 $R$ 的协方差矩阵为

$$ Var(R) = \begin{bmatrix} Var(R_1) & Cov(R_1, R_2) & \cdots & Cov(R_1, R_d) \\ Cov(R_2, R_1) & Var(R_2) & & Cov(R_2, R_d) \\ \vdots & & \ddots & \vdots \\ Cov(R_d, R_1) & Cov(R_d, R_2) & \cdots & Var(R_d) \end{bmatrix} $$

对于一个符合高斯分布的变量 $R \sim \mathcal{N}(\mu, \Sigma)$，有 $Var(R) = \Sigma$

如果两个随机变量 $R_i, R_j$ 独立，那么 $Cov(R_i, R_j) = 0$ （独立 $\Rightarrow$ 不相关）
如果 $Cov(R_i, R_j) = 0$，并且他们一起满足多维高斯分布，那么他们独立（高斯分布限制了只能存在线性关系+不相关 $\Rightarrow$ 独立）

如果 $Var(R)=\Sigma$ 是一个对角矩阵，并且满足多维高斯分布（向量中的每个元素互相独立）
$\Leftrightarrow f(R) = f(R_1)f(R_2)\cdots f(R_d)$
$\Rightarrow$ 椭球面是轴对齐的，并且 $\Sigma$ 的对角元素等于半径的平方