高斯判别分析 Gaussian Discriminant Analysis
基本假设:每个类别服从高斯分布
$$X \sim \mathcal{N}(\mu, \sigma^2): f(x) = \frac{1}{(\sqrt{2 \pi} \sigma)^d}\exp{\left( -\frac{\|x - \mu\|^2}{2\sigma^2} \right)}$$其中 $x,\mu$ 是向量,$\sigma$ 是标量,$d$ 表示维度。(注:这里使用的正态分布公式是一个简化版本,它假设数据在所有的特征维度上的方差相同,并且不考虑不同特征之间的相关性)
对于每个类别 $C$,假设我们知道了均值 $\mu_C$ 和协方差 $\sigma_C^2$,那么我们就可以根据上述高斯分布公式,将均值和方差代入确定概率密度函数 $f_{X|Y=C}(x)$。同时假设前验概率 $\pi_C=P(Y = C)$ 已知
在给定观测 $x$ 的条件下,贝叶斯决策准则 $r^*(x)$ 根据最大化 $f_{X|Y=C}(x)$ 来判决类别 $C$
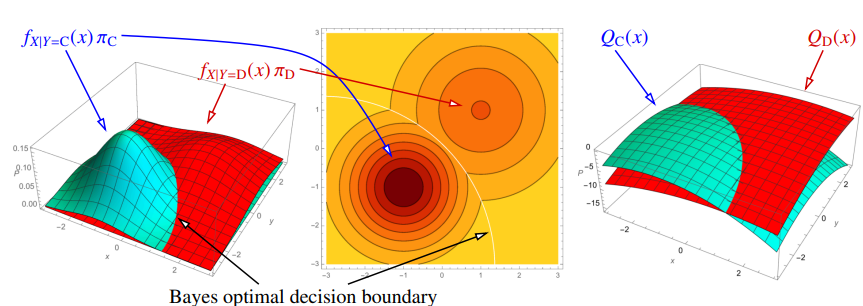
两个类别的概率密度函数
等价于最大化
$$Q_C(x) = \ln\left( (\sqrt{2\pi})^d f_{X|Y=C}(x) \pi_C \right)=-\frac{\|x - \mu_C\|^2}{2\sigma_C^2}-d\ln\sigma_C + \ln\pi_C$$$Q_C(x)$ 是一个关于 $x$ 的二次函数
二次判别分析 Quadratic Discriminant Analysis (QDA)
假设只有两个类别 $C$ 和 $D$,那么贝叶斯分类器为
$$ r^*(x) = \begin{cases} C & \text{if } Q_C(x) - Q_D(x) > 0 \\ D & otherwise \end{cases} $$决策函数为 $Q_C(x) - Q_D(x)$,贝叶斯决策边界为 $\{ x: Q_C(x) - Q_D(x) = 0 \}$。如果样本点是 $1$ 维的,那么贝叶斯决策边界可能有 $1$ 个或者 $2$ 个点(二次方程的解);如果样本点是 $d$ 维的,那么贝叶斯决策边界是一个二次曲面。
除了根据贝叶斯规则判别样本点的类别外,也可以得到判别正确的概率,即
$$P(Y = C | X = x) = \frac{f_{X | Y = C}\pi_C}{f_{X | Y = C}\pi_C + f_{X | Y = D}\pi_D}$$上式也可以进一步写成
$$P(Y = C | X = x) = \frac{e^{Q_C(x)}}{e^{Q_C(x)} + e^{Q_D(x)}} = s(Q_C(x) - Q_D(x))$$其中 $s(\gamma)=\frac{1}{1 + e^{-\gamma}}$ 是 Logistic 函数也即是 Sigmoid 函数
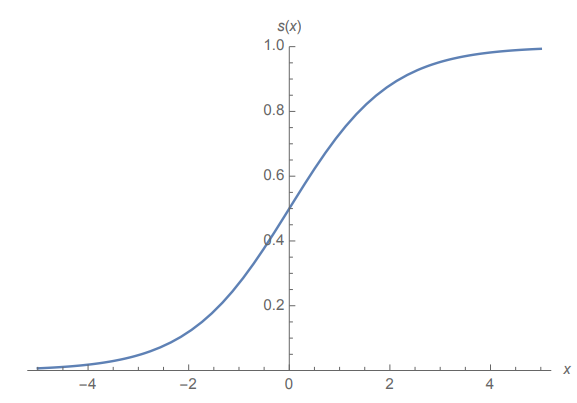
Logistic函数
Logistic 函数满足 $s(0) = 0.5$,也就是说当 $Q_C(x) = Q_D(x)$ 时,判别成两种类型的概率均等

多类别QDA判决边界
多类别 QDA 将特征空间划分为多个区域。在二维或更高维度中,通常会形成多个决策边界,这些边界在连接点处相互邻接
线性判决分析 Linear Discriminant Analysis (LDA)
LDA 时 QDA 的一个变种,它有线性的决策边界,相较于 QDA 不容易过拟合
基本假设:所有的高斯分布有相同的方差 $\sigma^2$
此时贝叶斯分类器是一个线性分类器
$$Q_C(x) - Q_D(x) = \underbrace{\frac{(\mu_C - \mu_D) \cdot x}{\sigma^2}}_{w \cdot x} \underbrace{- \frac{\|\mu_C\|^2 - \|\mu_D\|^2}{2\sigma^2} + \ln\pi_C - \ln\pi_D} _{+ \alpha}$$- 决策边界为 $w \cdot x + \alpha = 0$
- 前验概率为 $P(Y=C | X= x) = s(w \cdot x + \alpha)$
特殊情况:如果 $\pi_C = \pi_D = 0.5$,那么决策边界变为 $(\mu_C - \mu_D) \cdot x - (\mu_C - \mu_D) \cdot \left( \frac{\mu_C + \mu_D}{2} \right) = 0$,此时变成了质心法
多类别 LDA:选择类别 C,最大化线性决策函数 $\frac{\mu_C \cdot x}{\sigma^2} - \frac{\|\mu_C\|^2}{2\sigma^2} + \ln\pi_C$

多类别LDA决策边界
概率分布的参数估计
最大似然估计:通过选择使似然函数 $\mathcal{L}$ 最大化的参数来得到统计模型的参数估计值
估计前验概率 $\pi_C$
一个不均匀硬币,有概率 $p$ 得到正面,$1 - p$ 的概率得到反面。在 $n$ 次试验中,有 $a$ 次为正面,则似然函数为
$$\mathcal{L} = C_n^a p^a (1 - p)^{n - a}$$通过最大似然法,使 $\mathcal{L}$ 最大,$\frac{\partial \mathcal{L}}{\partial p} = 0$ ,得到 $p = \frac{a}{n}$
类似的,如果共有 $n$ 个训练样本点,其中 $a$ 个属于类别 C,则前验概率 $\hat{\pi}_C = a / n$
估计均值 $\mu_C$ 和方差 $\sigma_C^2$
根据 $n$ 个样本点 $X_1,X_2,\dots,X_n$ 求出最拟合的高斯分布
似然函数为
$$\mathcal{L}(\mu, \sigma;X_1,X_2,\dots,X_n) = f(X_1)f(X_2)\cdots f(X_n)$$为了方便计算,最大化对数似然函数
$$ \begin{align*} l(\mu, \sigma;X_1,\dots,X_n) &= \ln{f(X_1)} + \dots \ln{f(X_n)} \\ &= \sum_{i = 1}^n \left( -\frac{\| X_i - \mu\|^2}{2 \sigma^2} - d\ln{\sqrt{2\pi} -d \ln{\sigma}} \right) \end{align*} $$可得
$$ \begin{align*} & \nabla_ul = \sum_{i = 1}^n \frac{X_i - \mu}{\sigma^2} = 0 \quad \Rightarrow \quad \hat{\mu} = \frac{1}{n} \sum_{i = 1}^nX_i \\ & \frac{\partial l}{\partial \sigma} = \sum_{i = 1}^n \frac{\|X_i - \mu\|^2 - d\sigma^2}{\sigma^2} = 0 \quad \Rightarrow \quad \hat{\sigma}^2 = \frac{1}{dn} \sum_{i = 1}^n \|X_i - \hat{\mu} \|^2 \end{align*} $$对于 QDA,分别使用类别内的数据点每个类别 C 的均值和方差,使用所有数据点估计前验概率 $\hat{\pi}_C = \frac{n_C}{\sum_D n_D}$
对于 LDA,使用同样的方法估计每个类别的均值以及前验概率,然后使用所有数据估计方差
$$\hat{\sigma}^2 = \frac{1}{dn} \sum_C \sum_{\{i:y_i = c\}} \|X_i - \hat{\mu}_C\|^2$$