决策理论亦风险最小化
如果多个属于不同类别的样本点可能处于同一个位置(例如训练数据中,升高为 1.70m 的样本,可能男性和女性同样存在),此时我们没法通过一个分类器直接将样本划分为某一种类别,所以我们需要一个概率分类器,输出当前样本为某种类别的概率
贝叶斯定理:
$$P(Y| X) = \frac{P(X| Y) P(Y)}{P(X)}$$其中 $P(Y | X)$ 表示观测到 $X$ 的条件下事件 $Y$ 发生的后验概率,$ P(Y)$ 表示事件发生的先验概率。
例如,假设人群中 $10\%$ 的人患有癌症,$90\%$ 的人没有癌症,不同职业的人患有癌症的概率分布为
| job $(X)$ | miner $(X = 0)$ | farmer $(X = 1)$ | other ${} (X = 2)$ |
|---|---|---|---|
| cancer ${} (Y = 1)$ | $20\%$ | $50\%$ | $30\%$ |
| no cancer $(Y = -1)$ | $1\%$ | $10\%$ | $89\%$ |
我们可以计算出,农民没有癌症的概率为
$$P(Y = -1 | X = 0) = \frac{P(X = 0 | Y = -1) P (Y = -1)}{P(X = 0)}=\frac{0.1 \times 0.9}{0.1 \times 0.5 + 0.9 \times 0.1} = \frac{9}{14}$$在我们的概率分类器中,可能不同的错误判决类型带来的影响不同。例如将癌症判决为假阴性(本来有癌症但被判决为没有癌症)和假阳性(本来没有被判决为有)的后果差别非常大,前者会造成癌症被忽视,后者只会带来额外的检查开销。此时,我们可以通过损失函数衡量不同错误的代价
$$ L(\hat{y}, y) = \begin{cases} 1 & \text{if } \hat{y} = 1, y = -1 \\ 5 & \text{if } \hat{y} = -1, y = 1 \\ 0 & \text{if } \hat{y} = y \end{cases} $$其中 $\hat{y}$ 表示预测的类别,$y$ 表示真实的类别, 假阴性在损失函数中被施加了更多的权重,上述损失函数被称为是非对称的
相反的,一个对称的0-1 损失函数可以表示为
$$ L(\hat{y}, y) = \begin{cases} 1 & \text{if } \hat{y} \neq y \\ 0 & \text{if } \hat{y} = y \end{cases} $$定义 $r: \mathbb{R}^d \rightarrow \pm 1$ 是一个决策规则,也被称为分类器,它表示一个将特征向量 $x$ 映射到 1 或 -1 的函数
$r$ 的风险指在所有的可能的数据点 $(x, y)$ 上的期望损失
$$ \begin{align*} R(r) &= E[L(r(X), Y)] \\ &= \sum_x \left( L(r(x), 1)P(Y = 1 | X = x) + L(r(x), -1)P(Y = -1 | X = x) \right) P(X = x) \\ &= P(Y = 1) \sum_{x} L(r(x), 1) P(X = x | Y = 1) +\\ & \quad P(Y = -1) \sum_x L(r(x), -1) P(X = x | Y = -1) \end{align*} $$贝叶斯决策规则(贝叶斯分类器)就是可以最小化风险函数 $R(r)$ 的函数 $r^*$,当 $L(1, 1) = L(-1, -1) = 0$,即预测正确损失函数为 0 的情况下
$$ r^* (x) = \begin{cases} 1 & \text{if } L(-1, 1)P(Y = 1 | X = x) > L(1, -1)P(Y = -1 | X = x) \\ -1 & \text{otherwise} \end{cases} $$当损失函数 $L$ 是对称的时,$r^*$ 就是选择后验概率最大的类别
如果我们可以知道真实的概率分布,可以直接根据上式构建一个理想的概率分类器 $r^*$。但是真实场景中,我们只能通过一些统计手段估计概率分布
获得使风险函数最小的 $r^*$ 的过程被称为风险最小化
连续概率分布
假设 $X$ 有一个连续的概率密度函数,则
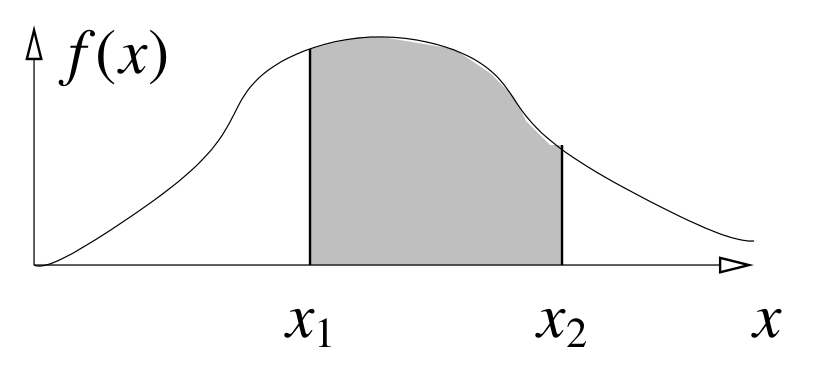
概率密度函数
- $X \in [x_1, x_2]$ 的概率为 $\int_{x_1}^{x_2} f(x) dx$
- 概率密度函数包含的整个区域面积为 $\int_{-\infty}^{\infty} f(x)dx = 1$
- $g(X)$ 的期望为 $E[g(X)] = \int_{-\infty}^{\infty} g(x)f(x) dx$
- $X$ 的均值为 $\mu = E[X] = \int_{-\infty}^{\infty}x f(x)dx$,方差为 $\sigma^2 = E[(X - \mu)^2] = E[X^2] - \mu^2$
假设我们使用 0-1 损失函数,在连续概率分布的情况下,此时贝叶斯决策规则为
$$ r^* (x) = \begin{cases} 1 & \text{if } f_{X | Y = 1}(x)P(Y = 1) > f_{X | Y = -1}(x)P(Y = -1) \\ -1 & \text{otherwise} \end{cases} $$上式表示,在观测到数据 $x$ 时,如果它有更多的可能为类别 1 则被判别为类别 1,反之不为类别 1
我们可以画出 $f_{X | Y = 1}(x)P(Y = 1)$ 和 $f_{X | Y = -1}(x)P(Y = -1)$ 的概率密度曲线
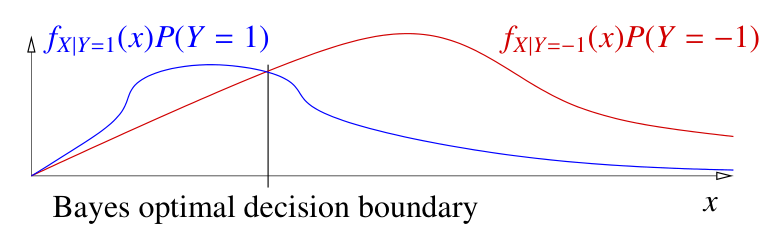
贝叶斯最优决策边界
贝叶斯决策规则对应了一个贝叶斯最优决策边界,即 $f_{X | Y = 1}(x)P(Y = 1) = f_{X | Y = -1}(x)P(Y = -1)$,它是两个概率密度函数的交点。在贝叶斯最优边界左边的点 $x$ 会被判别为类别 1,右边的点 $x$ 会被判别为类别 -1
贝叶斯最优决策边界是两个后验概率密度函数相交的边界,在这个边界上两者的概率密度相等,所以贝叶斯最优决策边界为 $\{ x: P(Y = 1 | X = x) = 0.5 \}$
在连续概率分布下,风险函数可以写成
$$ \begin{align*} R(r) &= E[L(r(X), Y)] \\ &= P(Y = 1) \int L(r(x), 1) f_{X | Y = 1}(x) dx + \\ & \quad P(Y = -1) \int L(r(x), -1) f_{X | Y = -1}(x) dx \end{align*} $$在 $r$ 为贝叶斯决策规则 $r^*$ 的条件下,贝叶斯风险就是两个概率密度函数重合部分的面积
$$R(r^*) = \int \min_{y = \pm 1} L(-y, y) f_{X |Y=y}(x) P(Y = y) dx$$构建分类器的三种方法
现在我们可以总结出三种构建分类器的方法:
- 生成模型 Generative models(例如LDA)
- 假设样本点来自特定的概率分布,并且不同类别的分布不同
- 猜测概率分布的形式
- 对每个类别,给定了概率分布的形式 $f_{X | Y = C}(x)$, 使得概率分布的参数拟合类别 C 的点
- 对每个类别 C 估计 $P(Y = C)$
- 根据贝叶斯定理计算 $P(Y | C)$
- 根据后验概率的大小,得出最终的类别,即使得 $f_{X|Y=C}(x)P(Y = C)$ 的 C
- 判别模型 Discriminative models(例如 logistic 回归)
- 直接对 $P(Y|X)$ 建模
- 寻找决策边界(例如 SVM)
- 直接对 $r(x)$ 建模
相较于方法 3,方法 1 和 2 都可以直接给出估计正确的概率。相较于方法 2,方法 1 一般在有异常值和少量训练样本下更加稳定,但是现实问题中很难准确估计概率分布
如果数据服从高斯分布或者一个特定的概率分布,一般使用生成模型效果更稳定
