机器学习问题的抽象
机器学习问题可以抽象成数据、模型、优化问题、优化算法四个层级
数据
数据是否有标签?
- 是:标签是类别(分类)还是数值(回归)
- 否:相似性(聚类)还是定位(降维)
模型
- 决策函数选择:线性、多项式、逻辑、神经网络,…
- 最近邻,决策树
- 特征选择
- 低容量 vs 高容量考虑(影响过拟合、欠拟合、推断)
最优化问题
变量、目标函数、约束条件
最优化算法
梯度下降、单纯形、SVD
最优化问题
无约束问题
目标:寻找一个 $w$ 最小化一个连续的目标函数 $f(w)$
如果 $f$ 的导数也是连续的则称 $f$ 是光滑的
全局最小值:对于任意 $v$,有 $f(w) \le f(v)$
局部最小值:一个 $w$ 附近的区间内,对于任意 $v$,有 $f(w)\le f(v)$
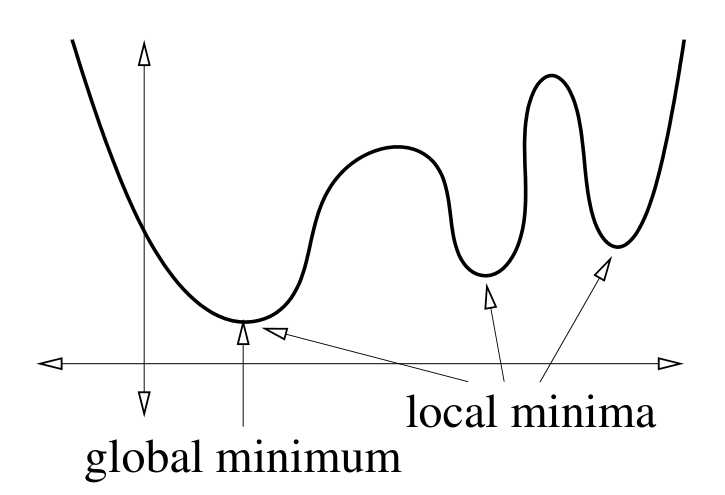
全局最小值和局部最小值
凸函数:函数 $f$ 是凸的,如果对于每个 $x, y \in \mathbb{R}^d$,连接 $(x, f(x))$ 和 $(y, f(y))$ 的切线在函数 $f$ 之上。
也可以表示为:对于任意 $x, y \in \mathbb{R}^d$,以及 $\beta \in [0, 1]$,有 $f(x + \beta(y - x)) \le f(x) + \beta (f(y) - f(x))$
凸函数的和也是凸函数。感知机的风险函数是凸损失函数的和,所以它也是凸函数。
一个连续函数如果在封闭的凸定义域内,则
- 没有最小值(趋近于 $-\infty$)
- 只有一个最小值
- 一个连通的最小值集合,且值相等(一个线段或者平面)
对于后两种情况,我们可以通过梯度下降法寻找最小值
很多时候我们没法找到一个凸目标函数,所以梯度下降只能找到一个局部最小值而不是全局最小值。但是在很多情形下,例如在训练神经网络时,随机梯度下降仍然是一个比较好的选择
线性规划
线性目标函数 + 线性约束函数
目标:寻找 $w$ 最大化(或者最小化)$c \cdot w$,并满足 $Aw \le b$
其中 $A$ 是一个 $n \times d$ 维度的矩阵,$b \in \mathbb{R}^n$。所以上述不等式包含了 $n$ 个线性约束
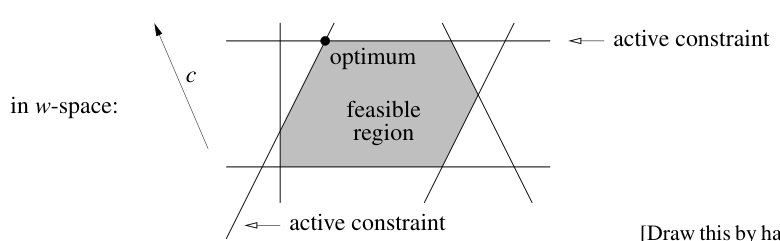
线性规划
满足所有约束条件的 $w$ 的集合是一个凸多面体,被称为可行域$F$。优化过程是在 $F$ 中寻找一个沿方向 $c$ 最远的点
凸多面体:对于任意 $p,q \in P$,连接 $p,q$ 的线段完全在 $P$ 内
在线性规划中,最优点通常位于边界或者顶点上,所以某些等式形式的约束被称为积极约束,积极约束对应的对偶变量通常非零。
在支持向量机中,在对偶问题中如果 $a_i > 0$,则原始问题中 $y_i (w^T x_i + b) = 1 - \xi_i$,所以支持向量在活跃约束上
线性规划最著名的算法是单纯性算法(simplex algorithm)
二次规划
二次凸目标函数 + 线性不等式约束
目标:寻找 $w$ 最小化 $f(w) = w^T Q w + c^T w$,并满足 $Aw \le b$
其中 $Q$ 是一个对称半正定矩阵
如果 $Q$ 是一个正定矩阵,目标函数是严格凸的,那么二次规划只有一个唯一的全局最优解(如果有解的话)。如果 $Q$ 是一个半正定矩阵,目标函数是凸的,但不一定是严格凸的,可能有多个目标函数值相同的全局最优解。如果 $Q$ 是非正定的,目标函数是非凸的,可能存在多个局部最优解,求解全局最优解通常是 NP-hard
