软间隔支持向量机
硬间隔 SVM 存在两个问题:
- 如果数据不是线性可分的,则算法将会失效;
- 对极端值(outliers)敏感,例如右图添加了一个极端值,严重改变了决策边界。
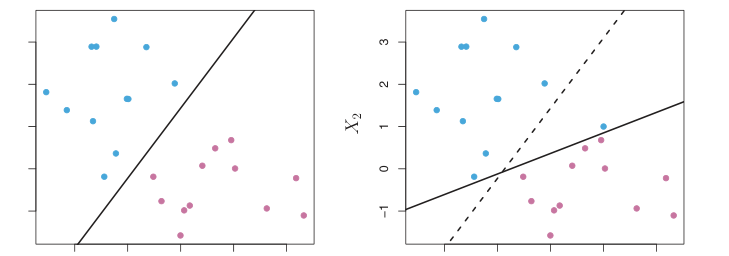
异常值造成了决策边界的偏移
软间隔支持向量机:通过引入松弛变量,允许一些样本点违背最小间隔的约束,此时约束条件可以变为
$$y_i (X_i \cdot w + \alpha) \ge 1 - \xi_i$$其中 $\xi_i$ 为引入的松弛变量,满足 $\xi_i \ge 0$。只有当样本点违背最小间隔约束时,松弛变量 $\xi_i$ 不为 $0$。
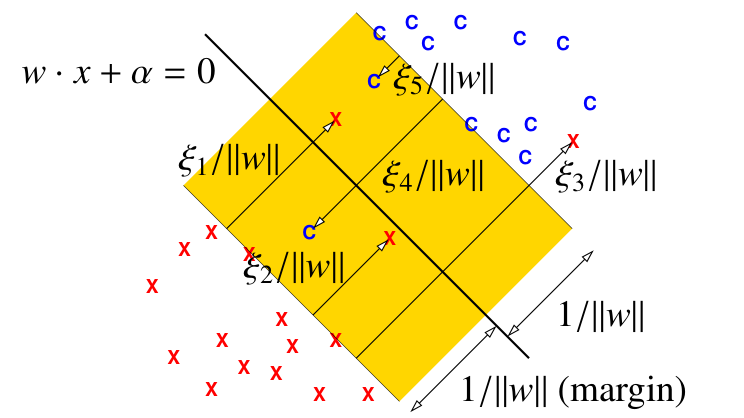
松弛变量存在的情况
此时,仍然定义间隔为 $1 / \|w\|$,为了防止松弛变量的滥用,我们在目标函数中添加一个损失项对其进行约束
$$ \begin{align*} & \text{Find } w, \alpha, \xi_i \text{ that minimize } \|w\|^2 + C\sum_{i = 1}^n\xi_i \\ & \begin{aligned} \text{subject to } & \quad y_i(X_i \cdot w + \alpha) \ge 1 - \xi_i & \text{for all } i \in [1, n] \\ & \quad \xi_i \ge 0 & \text{for all } i \in [1, n] \end{aligned} \end{align*} $$这是一个 $d + n + 1$ 维空间的、具有 $2n$ 个约束项的二次规划问题。其中 $C > 0$ 是一个正则化超参数(regularization hyperparameter)。
| 较小C | 较大C | |
|---|---|---|
| 目标 | 最大化间隔 ${} 1 / \|w\|$ | 保持大多数松弛变量为零或很小 |
| 风险 | 欠拟合(误分类许多训练数据) | 过拟合(训练效果好,测试效果差) |
| 异常值 | 不太敏感 | 非常敏感 |
| 边界(非线性时) | 更“平坦” | 更曲折 |
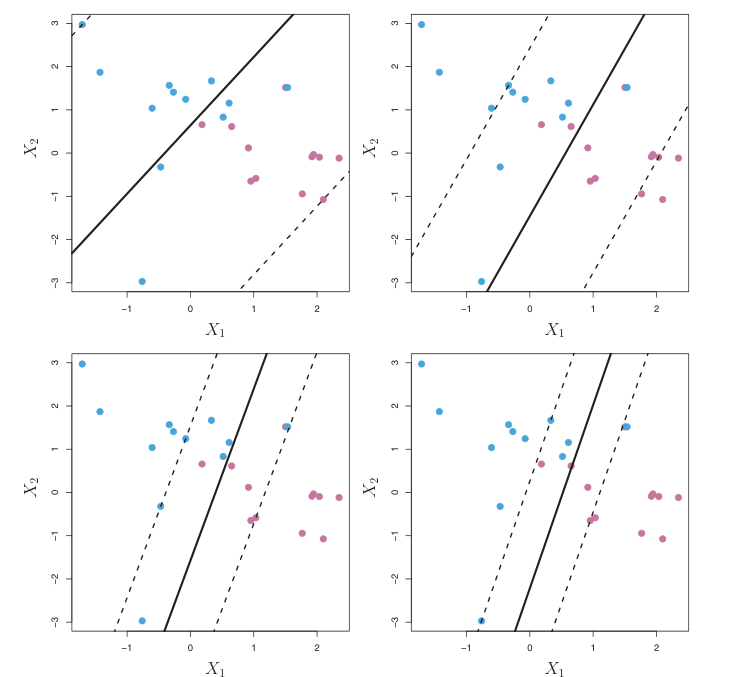
不同C值的决策边界,右下方C更大
特征与非线性
非线性决策边界:通过创建非线性特征将样本点提升到高维空间,那么高维的线性分类器等价于低维的非线性分类器
样例 1:抛物线提升映射(The parabolic lifting map)
定义一个非线性映射,将 $d$ 维空间的点 $x$ 提升为 $d + 1$ 维空间的抛物面
$$ \begin{align*} & \Phi: \mathbb{R}^d \rightarrow \mathbb{R}^{d + 1} \\ & \Phi(x) = \begin{bmatrix} x \\ \|x\|^2 \end{bmatrix} \end{align*} $$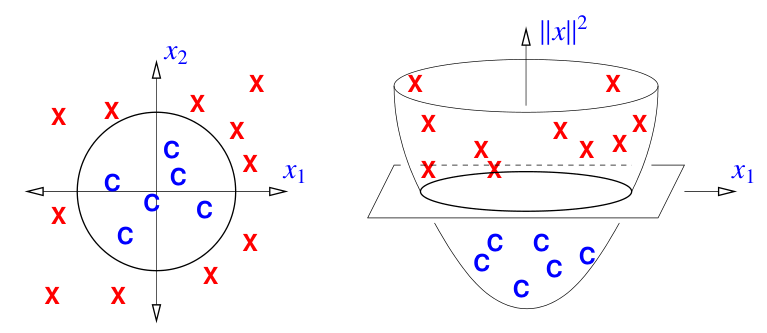
点被提升到抛物面
上图中样本点由二维空间的点,经过非线性映射被提升到三维空间的抛物面。此时二维平面的球形决策边界,等价于三维平面的线性决策边界。
定理:$\Phi(X_1),\Phi(X_2),\dots,\Phi(X_n)$ 线性可分 $\leftrightarrow$ $X_1,X_2,\dots,X_n$ 可以被超球面分离
证明:考虑 $\mathbb{R}^d$ 中的超球面,它的球心为 $c$,半径为 $\rho$。$x$ 在超球面内当且仅当
$$ \begin{align*} & \|x-c\|^2 < \rho^2 \\ & \|x\|^2 - 2c \cdot x + \|c\|^2 < \rho^2 \\ & \begin{bmatrix} -2c^T & 1 \end{bmatrix} \begin{bmatrix} x \\ \|x\|^2 \end{bmatrix} < \rho^2 - \|c\|^2 \end{align*} $$其中 $\begin{bmatrix}-2c^T & 1\end{bmatrix}$ 是 $\mathbb{R}^{d + 1}$ 中的法向量,而 $\Phi(x)$ 表示 $\mathbb{R}^{d + 1}$ 中的一个点,所以 $\mathbb{R}^{d}$ 中的超球面内等价于 $\mathbb{R}^{d + 1}$ 中的超平面以下。
样例 2:椭球体/双曲面/抛物面决策边界

不同的二次曲面
对于式
$$A x_1^2 + B x_2^2 + C x_3^2 + D x_1x_2 + E x_2x_3 + F x_3x_1 + G x_1 + H x_2 + I x_3 + \alpha = 0$$可以表示上图中的任意一个二次曲面。
所以,我们可以定义非线性映射
$$ \begin{align*} & \Phi(x) = \begin{bmatrix} x_1^2 & x_2^2 & x_3^2 & x_1x_2 & x_2x_3 & x_3x_1 & x_1 & x_2 & x_3 \end{bmatrix}^T \\ & \begin{bmatrix} A & B & C & D & E & F & G & H & I \end{bmatrix} \cdot \Phi(x) + \alpha \end{align*} $$此时,决策函数可以为任意二次多项式,决策超曲面可以为任意二次曲面。$\Phi-$ 空间的线性决策边界等价于 $x-$ 空间的二次曲面分类边界。
样例 3:$p$ 次多项式作为决策函数
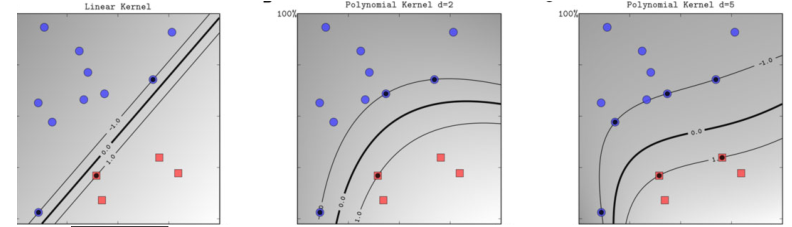
拥有不同次方的决策函数的硬支持向量机:1,2,5
增加决策函数的最高次
- 线性不可分的数据可能由于最够高的非线性变为线性可分
- 高维提供了更高的自由度,可能找到更大的间隔,可能提升决策边界的鲁棒性
核技巧
支持向量机的学习算法
在训练软间隔支持向量机时,我们可以使用如下学习算法(基于拉格朗日对偶性,推过过程参考李航-《统计学习方法》):
输入:训练数据集 $T={(x_1,y_1),(x_2, y_2),\dots,(x_n,y_n)}$,其中 $x_i \in \mathbb{R}^{d}, y_i \in \{-1,1\}$
输出:决策超平面和决策函数
(1)选择一个正则化超参数 $C > 0$, 求解以下凸二次规划问题(软间隔支持向量机的原始问题的对偶问题):
求解最优解 $\alpha^* = (\alpha_1^*, \alpha_2^*, \dots, \alpha_n^*)$
(2)计算 $w^* = \sum_{i = 1}^n \alpha_i^* y_i x_i$
选择一个下标 $j$,满足 $0< \alpha_j^* < C$,计算
(3)求得决策超球面
$$w^* \cdot x + b^* = 0$$以及决策函数
$$f(x) = w^* \cdot x + b^* = \sum_{i = 1}^n \alpha_i^* y_i(x \cdot x_i) + b^*$$在上述算法中,$w^*$ 和 $b^*$ 只依赖于 $\alpha_i^* > 0$ 的样本点 $x_i$,称这些样本点为支持向量。
可以看出在支持向量机学习算法中,无论优化的目标函数还是决策函数都只涉及两个向量之间的点积,例如 $x_i \cdot x_j$ 和 $x \cdot x_i$。
核函数
我们已经知道,低维空间的非线性决策曲面可以等价为高维空间的线性决策平面。
但是如果特征的维度 $d$ 非常高,此时使用非线性映射 $\Phi(x)$ 得到的高次多项式特征维度非常大,$\Phi(x_i) \cdot \Phi(x_j)$ 的计算复杂度非常大。
于是,我们希望找到一个低维空间核函数,等价于高维空间的点积运算
定义:设 $\mathcal{X}$ 是一个低维输入空间,$\mathcal{H}$ 是一个高维特征空间,如果存在一个映射
$$\Phi(x): \mathcal{X} \rightarrow \mathcal{H}$$使得对所有的 $x, z \in \mathcal{X}$,函数 $K(x, z)$ 满足
$$K(x, z) = \Phi(x) \cdot \Phi(z)$$则称 $K(x, z)$ 为核函数。
如果我们不显示指定一个非线性映射 $\Phi(x)$,而是使用一个特定的核函数 $K(x, z)$ 替代高维空间的点积 $\Phi(x_i) \cdot \Phi(x_j)$ ,那么支持向量机的优化目标可以写成
$$ \begin{align*} & \min_{\alpha} \frac{1}{2} \sum_{i = 1}^n\sum_{j = 1}^n\alpha_i\alpha_j y_i y_j K(x_i, x_j) - \sum_{i = 1}^n \alpha_i \\ &\begin{aligned} \text{s.t. } & \sum_{i = 1}^n \alpha_i y_i = 0 \\ & 0 \le \alpha_i \le C, \quad i = 1,2,\dots,n \end{aligned} \end{align*} $$此时我们可以在核函数 $K(x, z)$ 对应的高维特征空间 $\mathcal{H}$ 中寻找一个线性决策超平面,但是参数学习是在低维输入空间 $\mathcal{X}$ 进行的,这称为支持向量机的核技巧。
