感知机算法
在 机器学习 02 线性分类器和感知机——感知机中,我们将在 $x-$ 空间寻找分类超平面的问题转换为在 $w-$ 空间寻找一个最优点 $w$ 的问题。
| $x$-space | $w$-space |
|---|---|
| hyperplane: $\{ x : w \cdot x = 0 \}$ | point: $w$ |
| point: $x$ | hyperplane: $\{ z : w \cdot z = 0 \}$ |
- 在 $x-$ 空间的超平面被转换为在 $w-$ 空间的一个点,这个点是超平面的法线
- 在 $x-$ 空间的样本点被转换为在 $w-$ 空间的超平面,这个超平面的法线为样本点
如果我们需要找到的 $w$ 满足:当 $x$ 为类别 $C$ 时,$x \cdot w \ge 0$,那么
- 在 $x-$ 空间,存在一个超平面,分离了不同类别的点。所有属于类别 $C$ 的点与 $w$ 在超平面的同侧;所有不属于类别 $C$ 的点与 $w$ 在超平面的不同侧。
- 在 $w-$ 空间,每一个点 $X_i$ 对应了 $w-$ 空间一个超平面 $H_i$。如果 ${} X_i \in \text{class C}$,那么 $w$ 与 $X_i$ 在 $H_i$ 的同侧;反之,在不同侧。
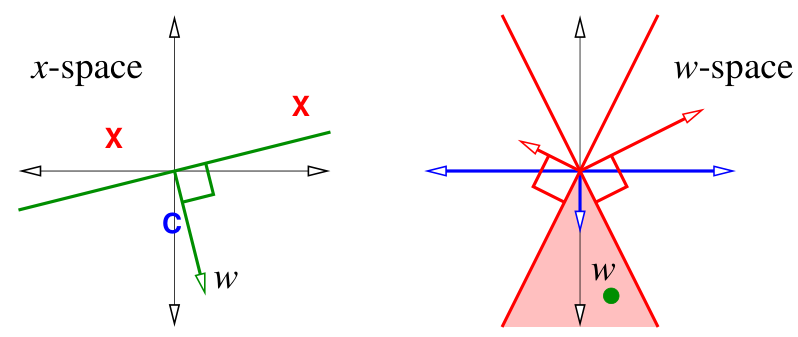
- 在左图中,$x-$ 空间内寻找一个超平面,可以将蓝色的样本点 $C$ (类别为 $C$ 的点)和红色的样本点 $X$ (类别不为 $C$ 的点)正确分类,$w$ 是这个超平面的法线。并且 $w$ 和样本点 $C$ 处于同侧。
- 在右图中,每一个样本点在 $w-$ 空间对应一个超平面,$w$ 需要处于红色超平面的反侧,处于蓝色超平面的正侧,即图中阴影区。
现在我们需要在 $w-$ 空间中找出最优的 $w$,使其最小化 $R(w)$ 。
优化算法:对风险函数 $R(w)$ 梯度下降
首先初始化 $w$ 的值,然后计算 $R(w)$ 关于 $w$ 的梯度(即 $R(w)$ 增长最快的方向),然后在相反的方向移动一步。
使用 机器学习 02 线性分类器和感知机——感知机 中定义的风险函数
$$R(w) = \frac{1}{n} \sum_{i = 1}^n L(X_i \cdot w, y_i) = \frac{1}{n} \sum_{i = 1}^n -y_iX_i \cdot w$$计算其梯度为
$$ \nabla R(w) = \begin{bmatrix} \frac{\partial R}{\partial w_1} \\ \frac{\partial R}{\partial w_2} \\ \vdots \\ \frac{\partial R}{\partial w_d} \end{bmatrix} = \nabla \sum_{i \in V}-y_i X_i \cdot w = -\sum_{i\in V}y_i X_i $$其中 $V$ 表示所有满足 $y_i X_i \cdot w < 0$ 的下标 $i$ 的集合。
对 $R(w)$ 的梯度下降可以表示为
$$ \begin{align*} & w \leftarrow \text{任意非零初始化} \\ & \text{while } R(w) > 0 \\ & \quad \quad V \leftarrow \text{所有满足 } y_i X_i \cdot w < 0 \text{ 的下标 } i \text{ 的集合} \\ & \quad \quad w \leftarrow w + \varepsilon \sum_{i \in V} y_i X_i \\ & \text{return } w \end{align*} $$其中 $\varepsilon$ 是学习率。
梯度下降的每一步复杂度为 $O(nd)$,我们可以通过随机梯度下降提升算法性能。
随机梯度下降的核心思想是在每一步的梯度下降中,随机选择一个满足条件的下标 $i$,并使用损失函数 $L(X_i \cdot w, y_i)$ 的梯度,该方法被称为感知机算法,其每一步的计算复杂度为 $O(d)$。
$$ \begin{align*} & \text{while } \text{找到某一个 } i \text{ 满足 } y_i X_i \cdot w < 0 \\ & \quad \quad w \leftarrow x + \varepsilon y_i X_i \\ & \text{return } w \end{align*} $$虽然随机梯度下降法非常高效,但是并不是所有梯度下降法可以解决的问题都可以使用随机梯度下降。 如果数据线性可分,感知机算法一定可以找到全局最优,随机梯度法一定可行。
如果我们需要找到不经过原点的超平面,此时只需要额外增加一个维度用于表示 $\alpha$
$$ f(x) = w \cdot x + \alpha = \begin{bmatrix} w_1 & w_2 & \alpha \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} $$此时我们的每个样本数据点存在于实数空间 $\mathbb{R}^{d + 1}$,其中最后一个维度的特征 $x_{d+1} = 1$。仍然可以在 $d + 1$ 维空间中使用感知机算法找到解。
感知机收敛理论:如果数据是线性可分的,感知机算法可以在最多 $O(r^2/\gamma^2)$ 的迭代中找到一个可以将所有数据正确分类的分类器。其中 $r=\max{\|X_i\|}$ 是数据的半径,$\gamma$ 是最大间隔。
最大边界分类器
一个线性分类器的间隔是超平面到最近的一个训练样本点的距离。如果我们可以找到一个超平面,它的间隔最大,那么这个分类器最优(决策边界离所有的点距离最远,最不容易分类错误)。
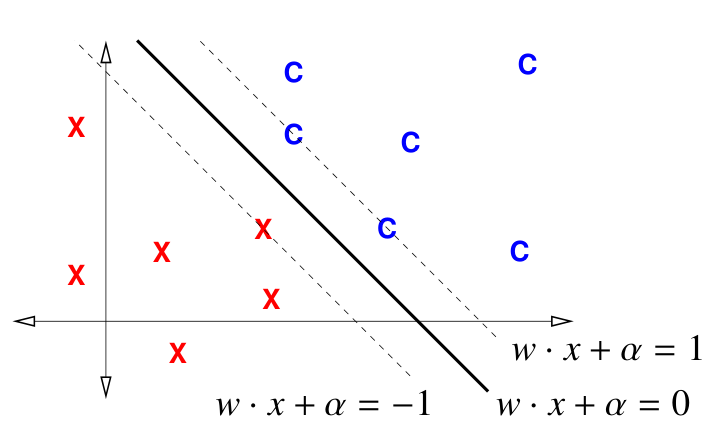
如图,一个满足上述条件的超平面可以表示为 $w \cdot x + \alpha = 0$,那么平行于这个超平面的、经过最近的样本点的超平面可以表示为 $|w \cdot x + \alpha| = 1$($1$ 只是为了方便讨论,也可以为 $w \cdot x + \alpha = k$,对 $k$ 归一化后也为 $1$)。
由于所有的样本点都在这两个最近超平面之外,所有样本点满足
$$w \cdot X_i + \alpha \ge 1 \quad \text{for } i \in [1, n]$$由于标签 $y_i \in \{1, -1\}$,约束条件可以表示成
$$y_i(w \cdot X_i + \alpha) \ge 1 \quad \text{for } i \in [1, n]$$已知,如果 $\|w\| = 1$,那么 $X_i$ 到超平面的有符号距离为 $w \cdot X_i + \alpha$。所以我们对 $w$ 归一化,可得
$$\frac{1}{\|w\|}|w \cdot X_i + \alpha| \ge \frac{1}{\|w\|}$$即间隔为 $\frac{1}{\|w\|}$,为了使间隔最大化,需要最小化 $\|w\|$。
于是可以求解优化问题
$$ \begin{align*} & \text{找到 } w, \alpha \text{ 最小化 } \|w\|^2 \\ & \text{同时满足 } y_i (X_i \cdot w + \alpha) \ge 1 \quad \text{for all } i \in [1, n] \end{align*} $$上述问题被称为在 $d + 1$ 维空间中,有 $n$ 个约束的的二次规划(quadratic program)。如果所有样本点线性可分,它有唯一解,反之无解。
最小化 $\|w\|^2$ 而不是 $\|w\|$ 的原因:$\|w\|$ 在 0 处不平滑。
上述方法可以得到一个最大间隔分类器,即硬间隔支持向量机(hard-margin support vector machine, SVM)。
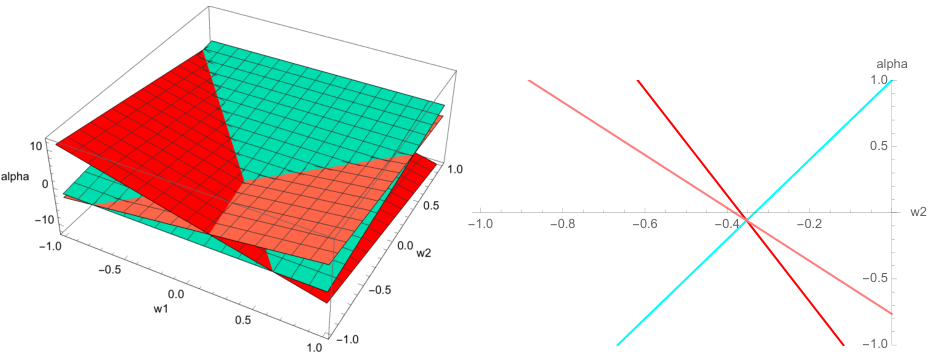
上图是 $(w_1, w_2, \alpha)$ 的三维空间。类别 $C$ 的样本点为法线的超平面为绿色,非类别 $C$ 的样本点为法线的超平面为红色。图中为 3 个样本点的情况。
- 为了满足约束条件 $y_i (X_i \cdot w + \alpha) \ge 1$,$w, \alpha$ 存在于绿色超平面之上,红色超平面之下
- 为了满足 $\|w\|^2$ 最小,$w, \alpha$ 应该最接近 $\alpha$ 轴
和感知机算法类似,只有所有数据点线性可分时,硬边界 SVM 可行。
