分类器
假设我们有 $n$ 个观测样例(bofservations),每个观测样例有 $d$ 个特征(features),有些样例属于类别 C,有些不是
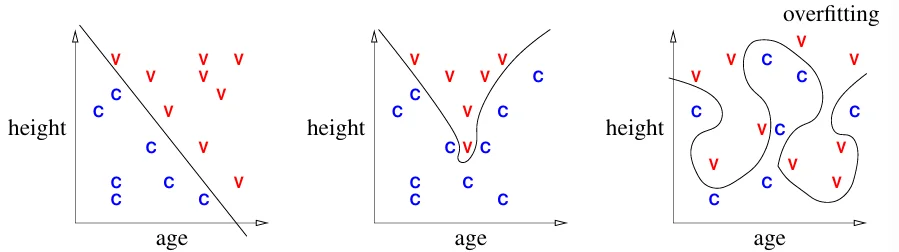
不同的决策边界
决策边界:分类器选择的可以将样例分成不同类别的边界
过拟合:决策边界拟合得太好,以至于无法用于未来样本的分类
决策函数:将一个点映射到一个值,例如
$$ \begin{matrix} f(x) > 0 & & \text{if } x \in \text{class } C; \\ f(x) \le 0 & & \text{if } x \notin \text{class } C; \end{matrix} $$则分类边界为 $\{x\in \mathbb{R}^{d}: f(x)=0\}$
分类边界
Linear Classifier Math
内积:$x\cdot y = x_1y_1+x_2y_2+\dots + x_dy_d$,也可以写成 $x^Ty$
欧拉范数:$\|x\|=\sqrt{x\cdot x}=\sqrt{x_1^2 + x_2^2 + \dots + x_d^2}$。可以表示向量 $x$ 的欧拉长度 (Euclidean length)。
归一化向量 $x$: ${x}/{\|x\|}$
给定一个线性决策函数 $f(x) = w \cdot x + \alpha$,决策边界为 $H = \{x: w \cdot x = -\alpha\}$。集合 $H$ 被称为超平面(hyperplane)。
- 超平面是 $d-1$ 维,并且分割了一个 $d$ 维空间
- 它是无限且平展的
$w$ 和超平面 $H$ 上的任何直线正交。所以 $w$ 被称为 $H$ 的法线(normal vector)。如果 $w$ 是一个单位向量,那么 $f(x) = w \cdot x + \alpha$ 是 $x$ 到 $H$ 的有符号距离(singed distance)。此外,$H$ 到原点的距离为 $\alpha$。
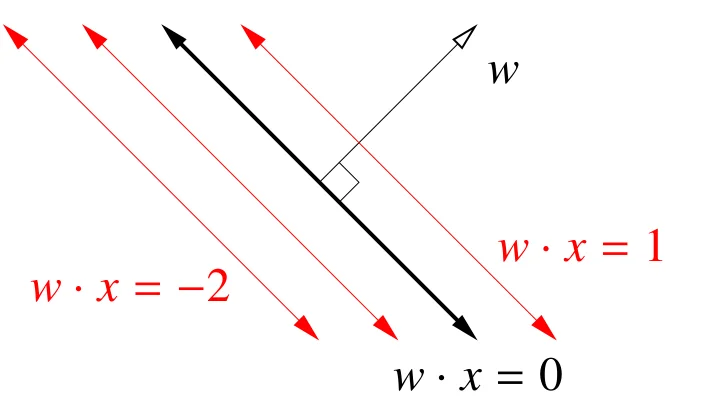
平面的法线
如果存在一个超平面可以将所有的训练样本点分类,则它们线性可分。
一个简单的分类器
质心法(Centroid method):首先分别计算属于类别 $C$ 的所有点的平均 $\mu_C$,以及所有不属于 $C$ 的平均 $\mu_X$。则决策函数可以表示为
$$f(x) = (\mu_C - \mu_X) \cdot x - (\mu_C - \mu_X) \cdot \frac{\mu_C + \mu_X}{2}$$质心法非常简洁,但是也只能处理简单的情况。例如下图中的数据点无法使用质心法正确分类。
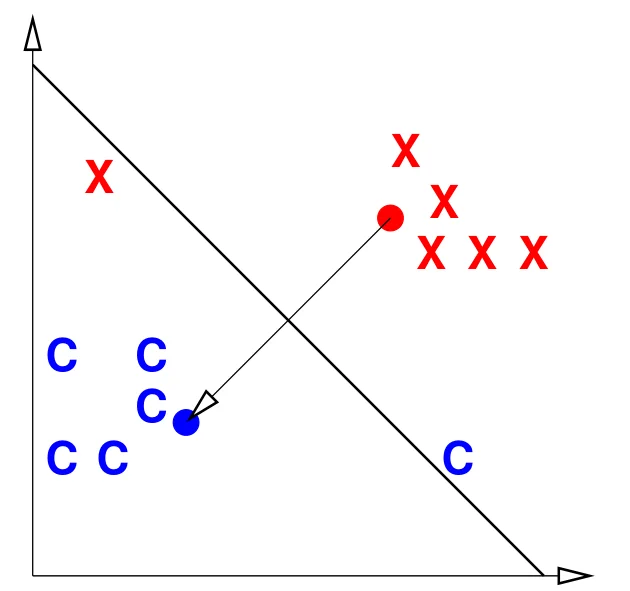
质心法失效的情况
感知机
假设有 $n$ 个采样点数据 $X_1, X_2,\dots,X_n$。对于每个采样点,对应的标签为
$$ y_i = \begin{cases} \begin{matrix} 1 & \text{if } X_i \in \text{class C} \\ -1 & \text{if } X_i \notin \text{class C} \end{matrix} \end{cases} $$为了简化讨论,这里只考虑经过原点的决策边界。于是我们寻找决策边界的目标可以转换成寻找一个权重 $w$,使其满足
$$ \begin{matrix} X_i \cdot w \ge 0 & & \text{if } y_i = 1 \\ X_i \cdot w \le 0 & & \text{if } y_i = -1 \end{matrix} $$等价为
$$y_iX_i\cdot w \ge 0$$上式即为约束(constraint)。
为了找到最优的 $w$,我们定义一个风险函数$R$,如果约束被违背,则风险函数为正值,然后通过最小化 $R$ 选择最优 $w$。
首先定义损失函数
$$ L(\hat{y}, y_i) = \begin{cases} \begin{matrix} 0 & & \text{if } y_i\hat{y} \ge 0 \\ -y_i \hat{y} & & \text{otherwise} \end{matrix} \end{cases} $$其中 $\hat{y}$ 是分类器的预测值。
于是,我们可以定义风险函数(即优化问题的目标函数)为
$$R(w) = \frac{1}{n} \sum_{i = 1}^n L(X_i \cdot w, y_i) = \frac{1}{n} \sum_{i = 1}^n -y_iX_i \cdot w$$所以寻找超平面的问题变为一个最优化问题:寻找 $w$ ,使得 $R(w)$ 最小。
